Artist's Statement

By

Prof. Alex J. Feingold

Department of Mathematical Sciences

Binghamton University

Background History

I am a mathematician, a Professor in the Department of Mathematical Sciences at Binghamton University, where I started as an Assistant Professor in 1979. My field is a branch of algebra with strong connections to mathematical physics, but I have often been able to use geometric ideas and intuition in my research. Many aspects of mathematics are related to art, and many artists have used concepts from mathematics in their work. But it is much more rare to find a mathematician actually doing art. Of course, most good mathematicians would say that they are doing art whenever they prove a beautiful theorem, but it is a kind of abstract art, which would be difficult for a non-mathematical audience to appreciate or understand!

Aside from the ``art" accomplished in my professional work, I have had an interest in making art through sculpture at least since 1978, when I met Prof. Helaman Ferguson at my first math conference. He was the first professor to invite me, as a new Ph.D., to give a talk at another university. At that time he was a professor at Brigham Young University in Provo, Utah, and he was kind enough to invite me to give a colloquium talk there. While staying at his house for a week, he showed me his garage workshop, where he worked on stone sculpture as a hobby. He gave me some soapstone and some simple hand tools, and showed me how to shape and polish it into my first stone sculpture, imitating one of his. I took some other stone samples home with me, and made a few more, including one small marble piece, which was much hard material to shape! Before that influential meeting, I found an exhibition of kinetic sound sculptures by Harry Bertoia at the Johnson Art Museum at Cornell University. I thought they were so interesting that when I returned to Drexel University (my first job in Philadelphia, 1977-79), I tried making some myself (with help from Stanley Cohen in their metal shop). My first attempt at making a kinetic sound sculpture was in brass, and the base plate warped badly from the heat of welding, but the result was still interesting. Others I made of iron with quite thin rods making a light sound. After moving to Binghamton in 1979, I made a few more sculptures of various kinds, stone, wood and metal. I donated a couple kinetic sound sculptures to the WSKG (local public TV/radio station) Art Auction, but was never able to sell any until I put pictures on my university webpage.

My friend Helaman gave up his position as Professor at Brigham Young University to pursue his sculpture fulltime as a profession. He moved to Laurel, Maryland, and began a new career. He has been very successful, and is one of very few people making mathematics into stone and bronze sculptures. He has been very important to me as a mentor, a friend and an inspiration, and his work is now on a very high and ambitious level, including large granite pieces by commission. One of his greatest sculptures is a bronze torus knot 24 feet in diameter on the SUNY Stony Brook campus near the Simons Center for Geometry and Physics. Some years ago I went to him with a question about how I might use bronze casting to reproduce copies of a mahogany wooden sculpture I had made. He suggested that I try to contact someone in the Art Department of my university, so that I might learn how to do such a thing myself, and not just take it to a foundry for others to copy. That led me to contact Prof. Jim Stark, whose open and welcoming attitude, and endless patience and good advice allowed me to seriously pursue my interest in sculpture for about ten years. In fact, using the facilities of the Binghamton University sculpture studio, I have been able to make many cast bronze and iron sculptures through the lost wax method, and a few by direct metal welding. I have exhibited some of my sculptures in Binghamton at the Art Mission/Art Theater, at the Broome County Public Library, at the Know Theater, and in the office of the Dean of Harpur College at Binghamton University. I have donated one of my bronze cast sculptures to the Max Planck Institute for Gravitational Physics (Albert Einstein Institute) in Potsdam, Germany. I also made and donated a bronze version of the logo of the Institute des Hautes Etudes Scientifiques in Bures-sur-Yvette, France. Inspired by the great work of Helaman Ferguson, I have carved torus knots from various kinds of exotic wood and some stone (marble or alabaster). More recently I have explored the use of 3D printing to make small versions of my mathematical sculptures, some in jewelry size which can be made of materials including alloys of steel, bronze, silver, gold. I have opened a shop to sell some of these on the website of a 3D printing company:

http://www.shapeways.com/shops/Feingold_Math_Art

There are many pictures and comments about my mathematical sculptures on my university internet webpages, which can be found using any browser at the address:

http://people.math.binghamton.edu/alex/

under the heading ``Mathematical Sculptures by Alex Feingold". I would like to begin with a statement of the goals and general philosophy behind my work.

General Goals and Philosophy

Mathematics is the main inspiration for my sculpture. I am certainly still trying to learn technique and craftsmanship, exploring my limits and capabilities. There seem to be a very large number of ideas from mathematics that lend themselves to expression in sculpture, not just simple geometry, but using concepts from quite advanced branches of math. I am very willing to study and learn from others, but I am trying to develop a unique voice and vision of my own. I like best those small sculptures that can be picked up and handled, so that the tactile impressions of the hands are just as important as the image seen by the eyes. Surfaces, edges, curvature and texture are the local characteristics felt, but the larger global design is what appeals to the intellect and connects to the wider world as well as to mathematical concepts. Motion and sound are wonderful when incorporated into a sculpture, and I would like to explore more ways of achieving that goal. I think my work will always be on the abstract side, being mostly inspired by such concepts and ideas rather than being representational. I appreciate all opportunities to exhibit my work, and hope to get reactions to it from those in the art community.

I am always glad of opportunities to exhibit my sculptures. Below I will give some details and descriptions of several of the pieces I have been able to exhibit, including the ideas behind the pieces. I include some figures and pictures of the pieces.

Descriptions and Organizing Concepts

Kinetic Sound Sculptures

I have already said that one of my early inspirations was seeing and hearing the kinetic sound sculptures (KSS) of Harry Bertoia. In case you are not familiar with these, let me describe them briefly, and then explain what I have done with the concept. Flexible metal rods are attached to a metal base plate in a pattern so that when they are pushed (by hand or by wind) the tops sway and hit each other, causing sound vibrations in the rods and base. The tops of the rods may carry thicker rods, giving the appearance of cattails, and changing the period of motion as well as the tone of the sound. The base plate usually rests on adjustable ``feet", screws which can be used to level or attach the sculpture on the floor or table, and which transmit the vibration. I always make my kinetic sound sculptures with a special symmetrical rod pattern that comes from my mathematical research area. For example, there is an eight dimensional Lie algebra (said to be of type A<sub>2</sub>) whose adjoint representation has weight diagram consisting of a regular hexagon including the point at the center. I have made several versions of that 7-rod KSS with different size top rods to give different sounds, all but one sculpture made from the same kind of silicon-bronze alloy used for casting in the sculpture studio, and one made from stainless steel. I usually make them by threading the rods, tops and bases so that the pieces can be screwed together, allowing disassembly for easy shipment. I have also made some 13-rod KSS where the rod pattern comes from the adjoint representation of the type G<sub>2</sub> Lie algebra, which consists of a central point surrounded by two hexagons of different sizes that fit together into a ``Star of David" shown in Figure 1 below. The mathematical symmetries of these patterns are captured by the Weyl group, which is a dihedral group depending on the shape. There are infinitely many different possible weight diagrams for each type of Lie algebra, but the patterns all have the same basic Weyl group symmetries. The largest one I ever made was a commission for a client in Chicago, designed for an outdoor garden and consisting of 27 rods based on a high dimensional representation of the type A₂ Lie algebra. The pattern of rods is shown below in Figure 2.

Here I am exhibiting a 7-rod KSS whose bronze base plate is mounted on a larger wooden base of polished black walnut which adds considerably to the appearance, sound and balance. Pictures of this piece are shown in Figure 3.

Figure 1: G₂ Weight Diagram – 13 Rod Pattern

Figure 2: Type A₂ Weight Diagram – 27 Rod Pattern

Figure 3: 7 Rod Hexagon KSS - Two Views

Knot Sculptures

Several of my sculptures are related to the topological theory of knots. A knot is a closed loop in space, which is considered nontrivial if it curves around in such a way that it cannot be continuously deformed into a simple circle. The simplest example of such a nontrivial knot is the trefoil knot. When making such a knot sculpture, one thinks first of choosing a shape for the cross-section, that is, the shape of a slice at any point of the curve, perpendicular to the path of the curve. I have made several sculptures based on the trefoil knot, the simplest just from a bent rod (left over from a KSS!) so the cross-section is just a circle. Another was cast with a cross-section consisting of three circles, but it is not just three parallel rods going around the knot separately. As they go around the knot, they twist relative to each other, so that after going around the knot once, the first rod leads into the second, the second into the third, and the third into the first, making a single rod that goes around the knot three times before closing the loop. This idea is related to the mathematical concept of a fiber bundle, used in differential geometry, where there is a big difference between the local and the global structure of a manifold.

Two of the trefoil knots I have made were directly inspired by one made by the sculptor John Robinson. He made the cross-section a rectangle, and twisted it so that the rectangle formed a Mobius strip, the famous one-sided figure made from a long strip of paper by curving it into a cylinder, but giving a half-twist before connecting the ends. I made one such Mobius trefoil in bronze by casting from a wax model, and another by using the oxy-acetelyne torch to heat and bend a steel bar into the twisted knot, finally welding the ends together. In each case, I wanted the piece displayed in such a way that it could rotate in space, and its reflection be seen from below, so I made a base plate as I have used in my KSS, with a single rod in the center, its top sharpened to a point, on which the knot is balanced. The plate is polished so the viewer sees the reflection of the knot, but in the steel version, the reflection was achieved by a sheet of plexiglass on top of the plate. When struck by a hammer (a short metal rod provided for that purpose), these knots produce a beautiful tone rich in harmonics as the vibrations travel around and around the knot in both directions! These sculptures should therefore be considered sound sculptures. Pictures of these are shown in Figures 4 and 5. I found that the sound is much better when these sculptures are hung from a wire, so I have modified the supporting vertical rod so that it curves up over the top of the piece, and a wire then supports the piece. The short rod is used as a hammer to make the knot ring.

Figure 4: Steel Trefoil Mobius Knot

Figure 5: Bronze Trefoil Mobius Knot

The third trefoil knot sculpture I have exhibited has the cross-section of a curve called a hypocycloid. It is the curve made by a chosen point on a moving circle of radius R as it rolls (without slipping) inside a larger circle of radius 3R. This curve looks like a triangle whose sides are slightly curved inward, and is shown in Figure 6. I made a bronze cast knot about 9" across with this hypocycloid cross-section, twisting as it goes around the knot in such a way that the edges made by the three vertices form one continuous edge that closes up only after three circuits of the knot. In the same way, the three surfaces made by the curving edges of the hypocycloid also form one continuous surface that takes three circuits of the knot to repeat, similar to the Mobius strip. I display this piece hanging over a base of polished black walnut, supported by a bronze rod bent into a parabola, held by a thin steel wire, but easily removed for handling. A short length of bronze rod is set in a hole in the base and can be removed and used as a hammer to strike the knot, producing a beautiful tone. The sculpture, which has been sold, is shown in Figure 7. Figure 8 shows a hanging bronze cast figure eight knot sound sculpture (with circular cross section). A figure eight knot is the next most complex knot beyond the trefoil knot. Figure 9 shows a hanging bronze cast (3,5) knot (with circular cross section). I will discuss this knot below in the section on torus knot sculptures.

Figure 6: Hypocycloid curve

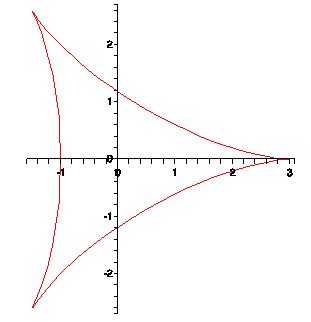
Figure 7: Bronze Trefoil Hypocycloid Knot

Figure 8: Cast Bronze Figure Eight Knot with circular cross section

Figure 9: Cast Bronze (3,5) Knot with circular cross section

Torus Knot Sculptures

From the first soft stone sculpture I made under the guidance of Helaman Ferguson, I have been inspired to make torus knots by carving and casting. A torus is a basic geometrical shape in mathematics, known more commonly as a doughnut. It is topologically distinct from a sphere because there are two circles on its surface, neither of which can be contracted to a point, one going around the hole, and one going through it. Any circle on a sphere can be continuously contracted to a point. A torus knot is a closed curve not crossing itself on the surface of a torus, and any such knot is topologically determined by an ordered pair of integers, (m,n), where m is the number of times the curve goes around the outside of the hole, and n is the number of times it goes through the hole. When making such a torus knot by carving or casting, it can be emphasized by making a valley in the surface of the torus so that the knot consists of the topmost points, the crest of two adjacent valley regions. For example, one can take the hypocycloid curve from Figure 6 and rotate it around a larger circle, keeping the hypocycloid perpendicular to the large guiding circle, but rotating it as it goes around. If it rotates by 120 degrees after one circuit, then a surface is created which Ferguson calls an ``umbilic torus", and the three cusp points of the hypocycloid trace out a (3,1) torus knot on that surface. With different amounts of rotation one makes different torus knots. I have made many with the (3,5) torus knot and some with the (4,5) torus knot. Figure 10 shows a (3,5) torus knot in cast bronze mounted on a bluestone base over a curved mirror, and Figure 11 shows a (4,5) torus knot in cast iron. Figure 12 shows a (4,5) torus knot carved from cocobolo wood. The wonderfully unique color and grain of each piece of wood makes each carving distinct, as can be seen in Figures 13 and 14.

Figure 10: Cast Bronze (3,5) Torus Knot

Figure 11: Cast Iron (4,5) Torus Knot

Figure 12: Carved Cocobolo Wood (4,5) Torus Knot

Figure 13: Carved Coolibah Burl Red (3,5) Torus Knot

Figure 14: Carved Tasmanian Eucalyptus Burl (3,5) Torus Knot

3D Printed Sculptures

The techniques of 3D printing are opening up a new world of opportunities for manufacturers and artists. I have started exploring these with the help and advice of several people, including Jonathan Clowes, who introduced me to the design program Rhinoceros3D, and Henry Segerman, who showed me how to incorporate Python code into Rhinoceros3D designs. My first goal was to make a 3D printed version of a Mobius figure eight knot with hypocycloid cross section, twisted so that it had only one side and one edge. I had already made a large one, about 18 inches across, by bronze casting. It was quite tricky to get this design into the computer so that it closed into a smooth surface. I finally was successful in Fall 2014, and a plastic version about 5 inches across is shown in Figure 15. Smaller jewelry size versions (about 1 inch across) are shown in Figures 16, 17 and 18, in bronze, rhodium plated brass, and rose gold plated brass.

Figure 15: 3D Printed Mobius Figure Eight Knot

Figure 16: 3D Printed Mobius Figure Eight Knot in Bronze

Figure 17: 3D Printed Mobius Figure Eight Knot in Rhodium Plated Brass

Figure 18: 3D Printed Mobius Figure Eight Knot in Rose Gold Plated Brass

My second 3D printed jewelry design was the (3,5) torus knot with circular cross section (which I call tubular) shown in Figure 9 in a large cast version. Figures 19, 20 and 21 show the 3D printed versions (about 1 inch across) in stainless steel, rhodium plated brass and

Figure 19: 3D Printed Tubular (3,5) Knot in Stainless Steel

Figure 20: 3D Printed Tubular (3,5) Knot in Rhodium Plated Brass

Figure 21: 3D Printed Tubular (3,5) Knot in Rose Gold Plated Brass

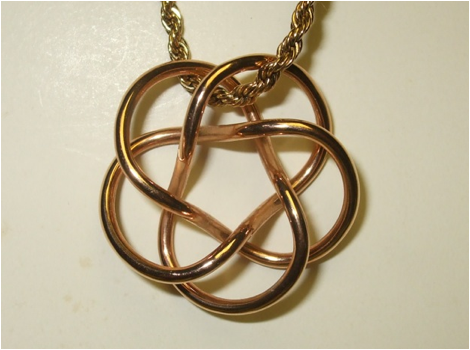
I used Python code to precisely describe the (3,5) torus knot surface which I have carved and cast so many times, but in order to 3D print it at such a small scale, the sharp edge forming the knot had to be rounded smoothly. I call the resulting piece a Python (3,5) Torus Knot Pendant. Figures 22, 23 and 24 show this pendant in stainless steel, polished nickel steel, and rose gold plated brass.

Figure 22: 3D Python (3,5) Torus Knot Pendant in Stainless Steel

Figure 23: 3D Python (3,5) Torus Knot Pendant in Polished Nickel Steel

Figure 24: 3D Python (3,5) Torus Knot Pendant in Rose Gold Plated Brass

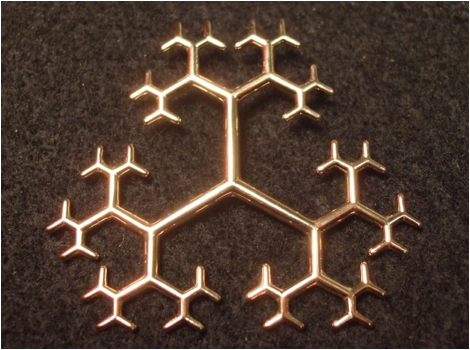
My most recent design for 3D printing is based on my current research into buildings for hyperbolic Kac-Moody groups. For such groups in rank 2 the building is a tree, that is, a graph of vertices and edges with no loops. The mathematical tree has infinitely many vertices and edges, with no end points (leaves), but my sculpture had to be finite and the edges had to get smaller towards the outside so as not to touch each other. The tree is determined by how many edges come out of each vertex, and in this design that number is three (except at the boundary), so it is call ``trivalent". Figure 25 shows my design of a trivalent tree pendant.

Figure 25: Trivalent Tree Pendant in RoseGold Plated Brass