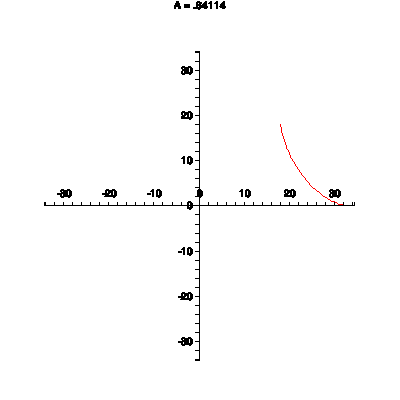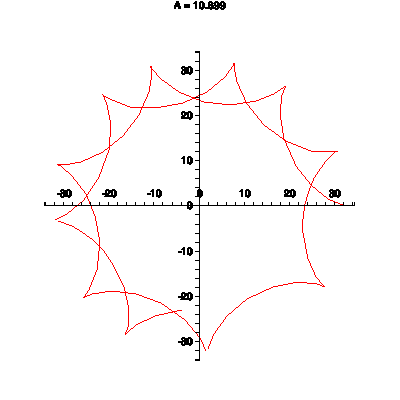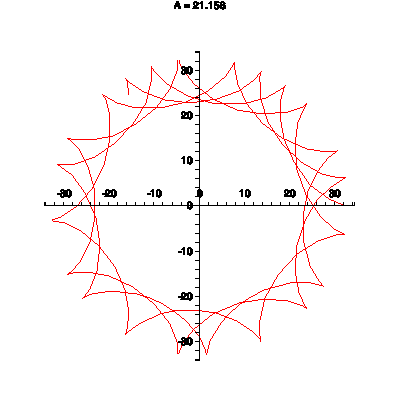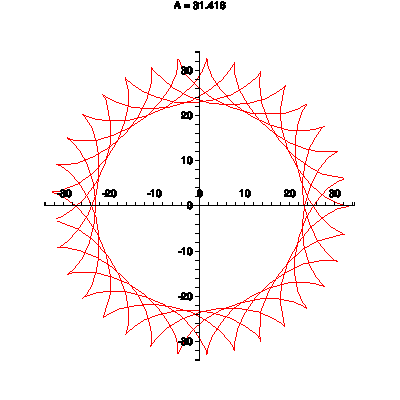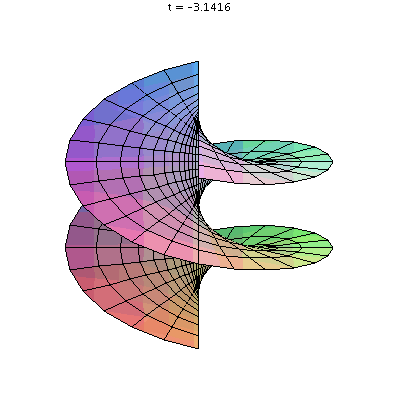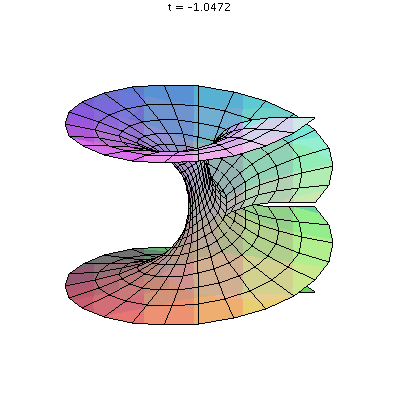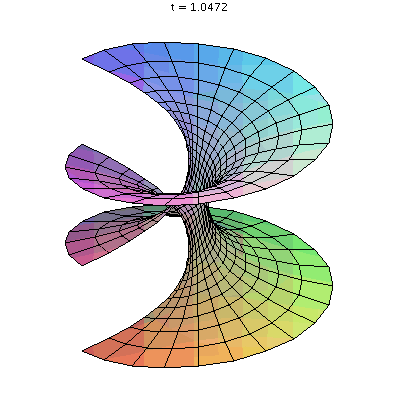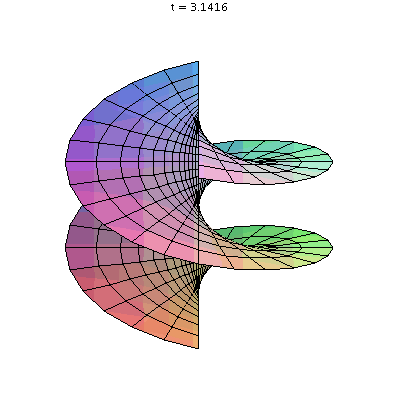Here are four cool animated GIFs by Fairy Suryana's Animated GIFs Gallery, a dragon by Boingdragon, a Quake III Arena icon, and a cool animated gif I found on the web of Felix the Cat (pacing back and forth, clearly thinking about a math problem), but I don't know who to give credit to for it:

A cool animated GIF of the cycloid x = r(t - sin(t)), y = r(1 - cos(t)) made by Maple.

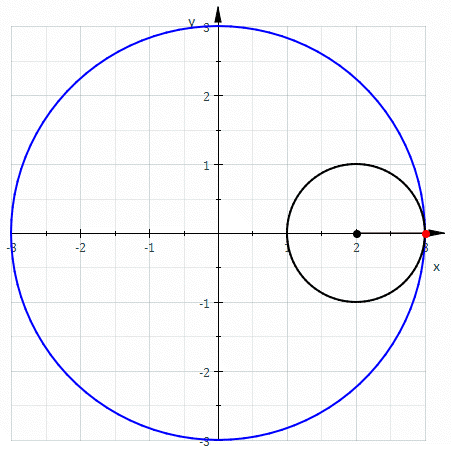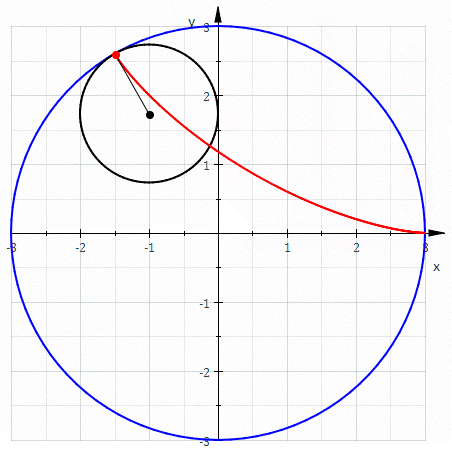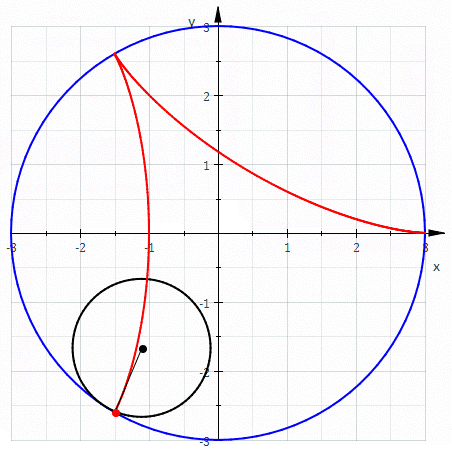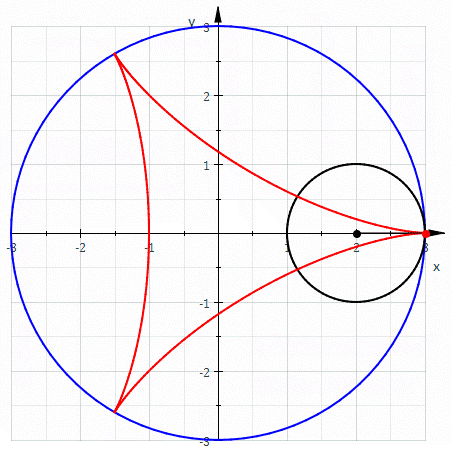
Another animated GIF made by Maple, the hypocycloid, where a smaller circle is running inside a bigger circle and comes back to its beginning after a finite number of steps. If the larger circle has radius R and the smaller circle has radius r, then parametric equations for the hypocycloid are x(t) = (R-r)cos(t) + r cos((R-r)t/r), y(t) = (R-r) sin(t) - r sin((R-r)t/r). If k = R/r, the equations can be written as x(t) = r(k-1)cos(t) + r cos((k-1)t), y(t) = r(k-1)sin(t) - r sin((k-1)t).

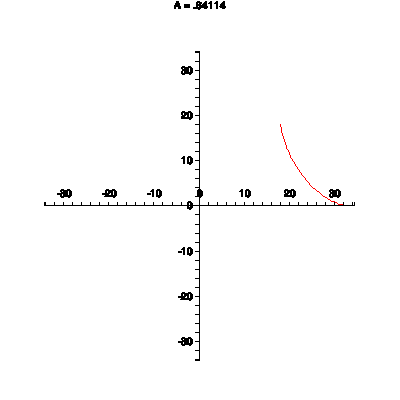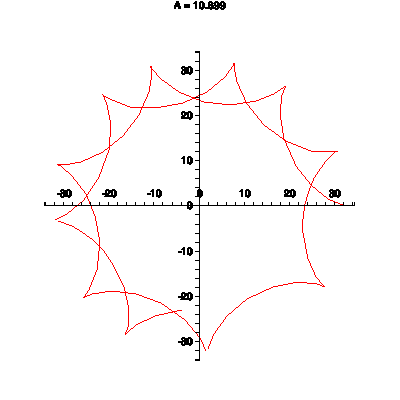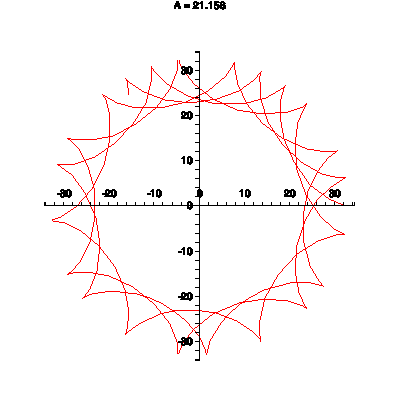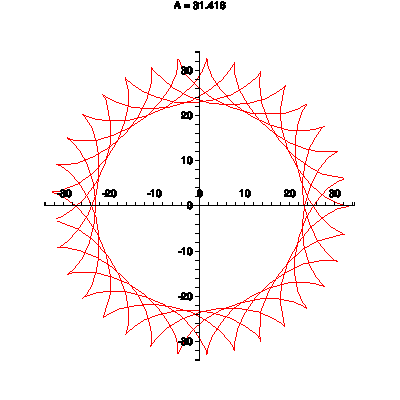
I found this animated GIF on wikipedia, showing the special case of the hypocycloid above where R=3 and r=1, so k = 3, making a single triangle inside the big circle before coming back to its beginning. This is also called a deltoid, and I have tried making sculptures of knots where this is the cross section of the knot.

An animated GIF showing the transformation of a helicoid to a catenoid made by Maple.

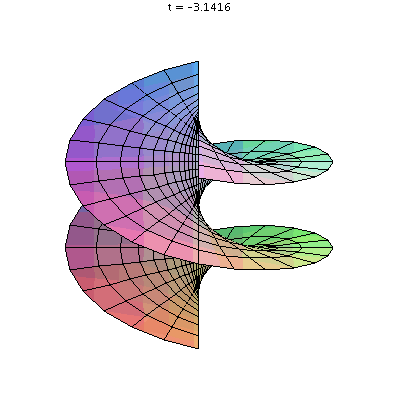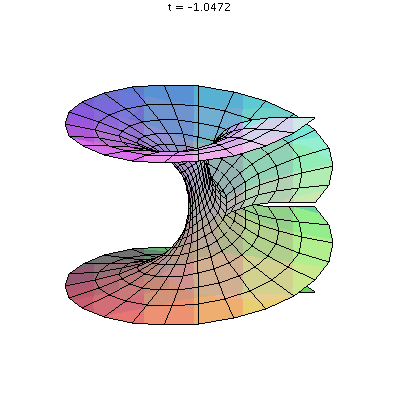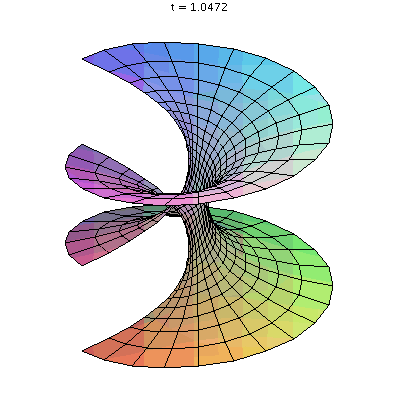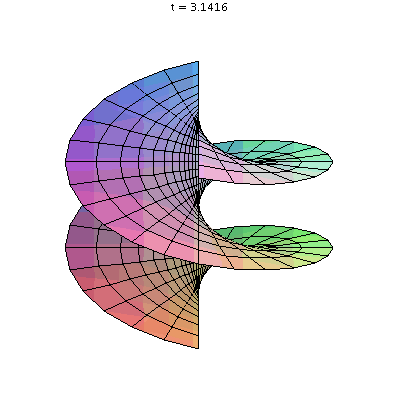
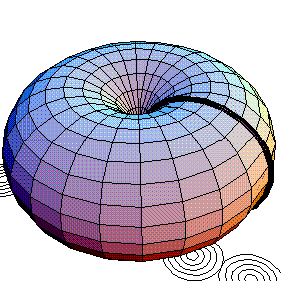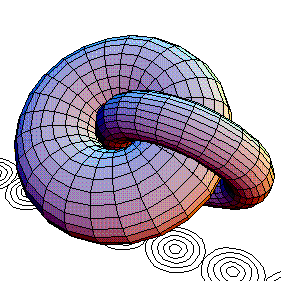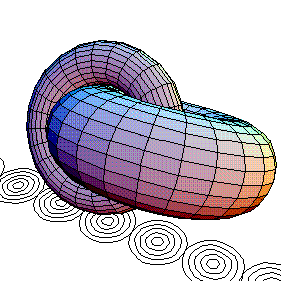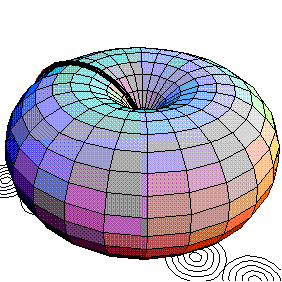
Another cool animated GIF of two tori made by Mathematica.

Links back to:
Alex Feingold's Webpage,
Department of Mathematical Sciences,
Binghamton University.