Section 3.4.
We work with the aluminum data in ALMPIN.mtw MTB > Retrieve 'C:\MTBSEW\INDUST~1\MTW\ALMPIN.MTW'. This data records of 6 dimension variables measured in mm of 70 aluminum pins used in airplanes, in order of production. The six variables are c2=diameter1, c3=diameter2, c4=diameter3, c5=cap diameter, c6=length of the pin without cap, c7=length of the pin with cap. c2 c3 and c4 give the pin diameter at three specified locations. c5 is the diameter of the cap at the top of the pin. c6 and c7 are the length of the pin without the cap and with the cap respectively. First, we find the sample covariances and correlations of C2-c7 MTB > covariance c2-c7 Diam1 Diam2 Diam3 CapDiam Leng_NCP Diam1 0.00026998 Diam2 0.00028323 0.00032441 Diam3 0.00025487 0.00028375 0.00027547 CapDiam 0.00029110 0.00031114 0.00028633 0.00036141 Leng_NCP -0.00016481 -0.00020445 -0.00014441 -0.00013789 0.00190693 Leng_WCP -0.00032568 -0.00040880 -0.00033282 -0.00032195 0.00154607 Leng_WCP Leng_WCP 0.00230697 MTB > corre c2-c7 Diam1 Diam2 Diam3 CapDiam Leng_NCP Diam2 0.957 Diam3 0.935 0.949 CapDiam 0.932 0.909 0.907 Leng_NCP -0.230 -0.260 -0.199 -0.166 Leng_WCP -0.413 -0.473 -0.417 -0.353 0.737 We should expect positive correlations between all the variables (large pins are large in all the dimensions). However, this does not happen. Some of the correlations are negative. We also can get multiple plots: MTB > matrixplot c2-c7
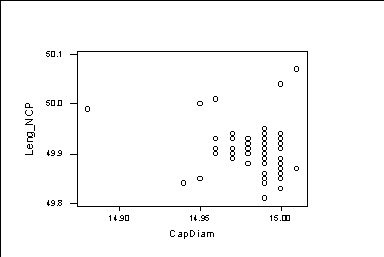
We see that some graphs show an isolated point. For example: MTB > plot c6*c5
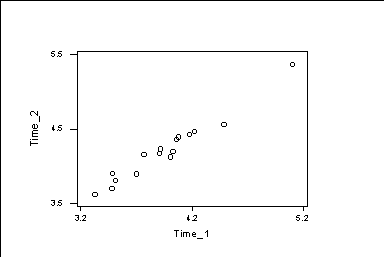
We have an isolated point on the left. We need to find the number of the observation giving the smallest value. MTB > rank c5 c15 MTB > print c15 MTB > set c16 DATA> 1:70 DATA> end MTB > sort c16 c17; SUBC> by c15. MTB > print c16 66 2 3 9 13 14 17 18 1 15 16 20 21 22 7 19 23 24 25 43 45 57 68 4 5 6 8 10 11 12 26 27 29 30 31 33 34 35 38 39 41 42 46 48 51 54 58 59 60 62 63 65 70 28 32 36 37 40 44 50 52 53 55 56 61 64 67 69 47 49 In the column c15, we get the ranks of the observations. In the column c17, we get the antiranks, the smallest c5 observation is in Y(c17(1)); the second smallest c5 observation is in Y(c17(2)); and so on. In this way, we get that the isolated observation is the number 66. The command: "sort c16 c17; by c15." orders the values of c16 in c17 according to the order in c15. In this way, we get that the isolated observation is the number 66. If we remove observation 66, we get bigger correlations MTB > delete 66 c2-c7 MTB > corre c2-c7 Diam1 Diam2 Diam3 CapDiam Leng_NCP Diam2 0.923 Diam3 0.922 0.937 CapDiam 0.875 0.838 0.874 Leng_NCP -0.103 -0.150 -0.093 -0.019 Leng_WCP -0.313 -0.396 -0.328 -0.229 0.720 Next, we work with the solar cells data. The data consists of the short circuit current of 16 solar cells measured in 3 different months. MTB > Retrieve 'A:\SOCELL.MTW'. We try to find the linear relation between t1 and t2. This is the graph of t1 and t2. MTB > plot c2*c1
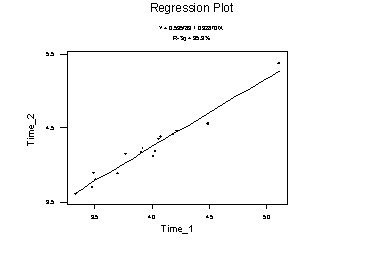
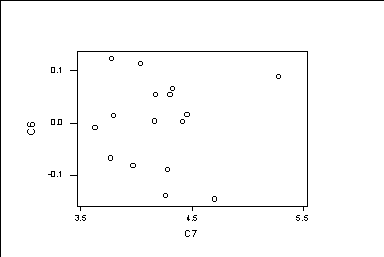
Next, we fit a regression line through this data: MTB > regre c2 1 c1; SUBC> resi c6; SUBC> fits c7. The regression equation is Time_2 = 0.536 + 0.929 Time_1 Predictor Coef Stdev t-ratio p Constant 0.5358 0.2031 2.64 0.019 Time_1 0.92870 0.05106 18.19 0.000 s = 0.08709 R-sq = 95.9% R-sq(adj) = 95.7% Analysis of Variance SOURCE DF SS MS F p Regression 1 2.5093 2.5093 330.84 0.000 Error 14 0.1062 0.0076 Total 15 2.6155 Unusual Observations Obs. Time_1 Time_2 Fit Stdev.Fit Residual St.Resid 9 5.11 5.3700 5.2814 0.0628 0.0886 1.47 X X denotes an obs. whose X value gives it large influence. ************************************************************ We obtain the linear regression equation, a table of coefficients, an estimate of standard deviation about the regression line, the coefficient of determination (R-squared), R-squared adjusted for degrees of freedom, the analysis of variance table, and unusual observations. First, we get the least squares regression line y=a+bx, in this case: Time_2 = 0.536 + 0.929 Time_1 a is the constant term and b is the slope. Then, we get columns related to the estimators a and b. The column coefficients gives the estimates (a and b) of the linear equation. The column Stdev gives estimates of the standard deviation of the coefficients. This measure how precise our estimators are. In this case the estimation of the constant term is not very precise, since Stdev=0.2031 and constant=0.5358. But, the estimation of the slope is very precise: b=0.92870 and its Stdev=0.05106 Next, we get the standard error s (the standard deviation of the residuals around the regression line), the coefficient of determination R-sq and the adjusted coefficient of determination R-sq(adj). R-sq measures the proportion of variation which has been reduced by the regression. Next, we get the analysis of variance table with degrees of freedom (df), sums of squares (SS) and mean square errors (MS). SOURCE DF SS MS Regression 1 SSR MSR Error n-2 SSE MSE Total n-1 SST To find this table, we use the fits hat-y_i=a+bx_i SSR=sum_i (hat-y_i - y-bar)^2 SSE=sum_i (y_i - hat-y_i)^2 SST=sum_i (y_i - y-bar)^2 We have that SST=SSR+SSE The column mean square is obtained dividing the mean square error over the degrees of freedom: MS=SS/df. MSR=SSR/1 MSE=SSE/(n-2). We have that the MSE=0.0076=s^2=0.08709^2. We have that the coefficient of determination R-sq=1-(SSE/SST) Note that SSE/SST is the proportion of the variation (or sums of squares) which is left after the regression. So, R-sq=1-(SSE/SST) is the proportion of variation which is explained by the liner regression model. We also have that R-sq=(correlation between X and Y)^2 Similarly, the adjusted coefficient of determination is R-sq(adj)=1-(MSE/MST) is the proportion of the mean squares which is left after the regression. Finally, we get the observations which are either influential or outliers. We could either X or XX for influential observations. We could get either R or RR for outliers. ********************** The subcommand SUBC> resi c6; put the residuals in the column c6. The subcommand SUBC> fits c7. put the fits in the column c7. ************************************************************************** Next, we get the graph of residuals versus predicts. MTB > plot c6 * c7
We should get a random graph. Values with a big residual are outliers. The macro %Fitline graphs the pairs of observations and the regression line. MTB > %Fitline 'Time_2' 'Time_1'