MATH. 341. Test No. 1. September 25, 1998

                                                                          

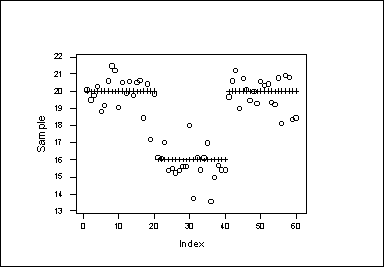
Name:  Miguel A. Arcones 



Answer all Questions.



1. The following graph shows a sample of 100 observations. What can you say 

about the structure of these observations?









Answer: There is a shift in the mean of the observations, 

happening during the observations 20-th to 40-th. 

During the first 19  observations the mean is 20. 

From the observation 20th to the observation

40-th the mean is 16. From the observations 41 on, the mean is again 20.

There exists a change of mean during a part of the observations.



2. What is the difference between random sampling with replacement (RSWR) 

and random sampling without replacement (RSWOR), when we sample 

10 items from a lot of 100 items?



Answer: When we sample without replacement, we cannot get again values which

we already got. However, when we sample with replacement, we can a value

several times.



3. The following is the frequency distribution of the number of blemishes, 

X, in a sample of size n=100 of ceramic plates purchased for hybrid 

microelectronic components.



ROWS: Nu_Blem.

 

  

 X        f              p             P

______________________________________________________________________

  0        2

  1        8

  2       17

  3       17

  4       22

  5        8

  6       18

  7        4

  8        1

  9        3

 10        0



ALL     100



a) Complete the above table by computing the column of proportional 

frequencies, p, and cumulative proportional frequencies, P.



b) What proportion of ceramic plates in the sample have at most 1 blemish?



c) What proportion of sample plates have between 2 and 5 blemishes?







Answer: 



(a)

(b) The proportion of ceramic plates in the sample which have 

at most 1 blemish is 0.02+0.8=0.10.



c) The  proportion of sample plates which have between 2 and 5 blemishes is

0.17+0.17+0.22+0.08=0.64.



4. In the Steel Rod data there are n=50 values. The following are 

some of the ordered values:

X(12) = 19.0839

X(13) = 19.1857

X(25) = 19.7656

X(26) = 19.8606

X(38) = 20.6091

X(39) = 20.6833



Compute the first quartile Q1, the Median Me, and the third quartile Q3.





Answer:



Q1 = X((n+1)/4)=X(12.75)

=(1-.75)X(12)+(.75)X(13)

=(1-.75)19.0839+(.75)19.1857=19.16025




Me =X((n+1)/2)=X(25.5)

=(1-.5)X(25)+(.5)X(26)

=(1-.5)19.7656+(.5)19.8606=19.8131




Q3=X((3(n+1)/4)=X(38.25)

=(1-.25)X(38)+(.25)X(39)

=(1-.25)20.6091+(.25)20.6833=20.62765




5. The following are the descriptive statistics of the yarn strength data file:



 Descriptive Statistics



Variable        N     Mean   Median   TrMean    StDev   SEMean

Yarnstrg      100   2.9238   2.8331   2.8982   0.9378   0.0938



Variable      Min      Max       Q1       Q3

Yarnstrg   1.1514   5.7978   2.2789   3.5732



Answer the following questions:



a) Why is the Mean different than the TrMean?



b) What will be the value of the sample mean if the maximal value 

in the sample will be changed to 6.53 ?



c) What is the value of the sample variance?



d) What is the value of the Inter-Quartile range IQR ?



e) Are there outliers in the sample? Justify your answer.



Answers:



a)   The sample mean is the average of all the values in the sample.

The trimmed sample mean is the average of the values in the sample, 

which are left after removing the 5 % smallest and the 5 % biggest

observations.



b) New Mean =2.931122

We change the maximum from 5.7978 into 6.53. 

So, the sum of the observations is increased by 6.53-5.797=0.7322.

The average, which is the sum of the observations over n, is increased by

0.007322.

So, the new mean is 2.9238+0.007322=2.931122



c) s2=0.8704688

The sample variance is the square of the standard deviation, in this case

0.93782=0.87046884



d) IQR =1.2943

The interquantile range is Q3-Q1=3.5732-2.2789=1.2943  



e) Outliers are values outside the interval determined 

by the lower and upper limits:



Lower Limit:   Q1 - 1.5 (Q3 - Q1)=2.2789-1.5(1.2943)=0.33745



Upper Limit:   Q3 + 1.5 (Q3 - Q1)=3.5732-1.5(1.2943)=5.51465



Since the minimum is 1.1514 and the maximum is 5.7978,

we have outliers in the sample.   





6. The plot below presents the scatterdiagram of the variables:

X: Turn Diameter (meters)

Y: HorsePower

In the CAR data.

The correlation between these two variables is R= .508.



a) What proportion of the total variability in HorseP is explainable 

by the linear regression of HorseP on TurnD?



b) The means and standard deviations of HorseP and TurnD are:



Mean of TurnD   =      35.514



Standard deviation of TurnD   =      3.3208



Mean of HorseP  =      124.67



Standard deviation of HorseP  =      40.162



What are the intercept and slope of the regression line of HorseP on TurnD?



c)   What is the predicted value of HorseP for a car having  

TurnD = 38 (meters)?







Answers:



a) Proportion of Variability Explained =Rx,y2=

 .5082=0.258064. 



b) Intercept =-93.3575; Slope =6.1392.



We have that b=Rx,ySy/Sx

=.508·40.162/3.3208=6.1392



a="y-bar"-b"x-bar"=124.67-(6.1392 ·35.514)=-93.3575

      

c)   Predicted HorseP =139.932



The least squares regression line is y=-93.3575+6.1392 x.

So, the Predicted HorseP when TurnD = 38 (meters) is

y=-93.3575+(6.139· 38)=139.932.