MATH. 341.   Test No.1. Solutions.    October 2, 2000



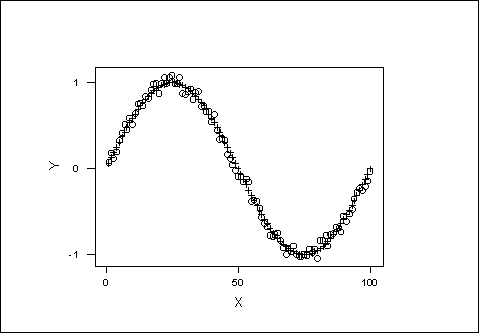
1. (10 points) .The following graphs show the measurements of the same sample of 100 observations, on two different instruments. In these measurements, Y=f(x)+E, where
f(x)=sin(pi x/50) and E is a random component.
 

         Instrument 1


 

 Instrument 2


 

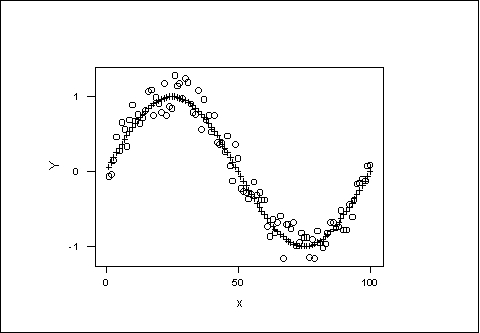
Which one of the two instruments is more precise?  (justify your answer).

Answer:
  Instrument 1 is more precise. According to the graphs, the dispersion of E in instrument 1 is smaller than that of instrument 2.
 

2. (10 points). The variables X1 , X2 ,..., X10 can each assume the values 0 or 1.

(i) How many possible binary signals are there, consisting of 5 of these variables?
(ii) How many binary signals of 10 variables have exactly 3 1’s?

Answer:

(i) 25=32

(ii) C103=120
 

3. ( 15 points). The following is the frequency distribution of the Turn Diameter in the Car data
 

X f p P
28-30 3 0.0275 0.0275
30-32 16 0.1468 0.1743
32-34 16 0.1468 0.3211
34-36 26 0.2385 0.5596
36-38 20 0.1835 0.7431
38-40 18 0.1651 0.9082
40-42 8 0.0734 0.9816
42-44 2 0.0184 1.0000
ALL 109 1.00 1.00

a) Complete the above table by computing the column of proportional frequencies, p, and cumulative proportional frequencies, P.
b) What proportion of cars have Turn Diameter between 35 and 39, inclusive? (interpolate if necessary)
c) Estimate the first, second and third quartiles.

Answers:

( b ) By interpolation
13 observations are in the interval (35,36];
20 observations are in the interval (36,38];
09 observations are in the interval (38,40].
So, the proportion of observations in the interval (35,39] is (13+20+9)/109=.3853

( c ) With X=32, we only get 17.43 % of the observations, with X=34, we get 32.11% of the observations. We need to increase the cumulative frequency by a percentage of (.25-.1743)/(.3211-.1743).
Since, we are increasing two units from X=32 to X=34, we have that

Q1=32+2(.25-.1743)/(.3211-.1743)=33.20

Similarly

Me=34+2(.50-.3211)/(.5596-.3211)=35.5

Q3=38+2(.75-.7431)/(.9082-.7431)=38.08

4. ( 15 points). In the YarnStrg data there are n=100 values. The following is the stem-leaf diagram of the data.

Stem-and-leaf of Yarn-Str  N  = 100
Leaf Unit = 0.10
 

    5     1  11344
   15    1  5556677788
   34    2  0011112222233344444
  (21)  2  555555555566677888999
   45    3  000011112223344444
   27    3  5556666677789
   14    4  00013344
    6     4  5668
    2     5  0
    1     5  7

Compute the first quartile Q1, the Median Me, and the third quartile Q3.

Answer:

Q1 = X((n+1)/4) =X(25.25)=(.75)X(25) +.25X(26)=2.2

Me = X((n+1)/2)=X(50.5) =(.5)X(50)+(.5)X(51) =2.28

Q3= X((3/4)(n+1)) =X(75.75)=(.25)X(75) +(.75)X(76)=3.5
 

5. ( 25 points). The following are the descriptive statistics of the steelrod data file:
 

Descriptive Statistics
 

Variable        N     Mean   Median   TrMean    StDev   SEMean
SteelRod       50   19.890    19.813   19.893    1.123    0.159

Variable      Min      Max       Q1       Q3
SteelRod   17.388   22.400   19.160    20.628

Answer the following questions:

a) If the five largest observations in the data set will be increased by 10 each, what will be the value of  Q1 and of Q3  ?
b) What will be the value of the sample mean if the largest value in the sample would be trimmed ?
c) What is the value of the inter-quartile range?
d) How many observations are greater than Q1 ?
e) Are there outliers in the sample? Justify your answer.
 

Answer:

a) Since Q1=X(12.75) and Q3=X(38.25), the values of Q1 and Q3 after changing the five largest observations are the same as before. Q1=19.160 and Q3=20.628

b) New Mean = the total sum is 994.5. If we remove the max which is 22.4 we are left with 972.1. The average for the left observations is 972.1/49=19.8387

c) IQR= Q3-Q1=20.628-19.160=1.468

d) number of observations larger than Q1 =50-12=38. Since Q1= X(12.75), there are 12 observations smaller than Q1 and 50-12=38 observations bigger than Q1.

e) The lower limit is Q1-1.5 IQR=16.958 and the upper limit is Q3+1.5 IQR=22.83. Since the lower limit is smaller than the minimum and the upper limit is bigger than the maximum, there is no outliers.

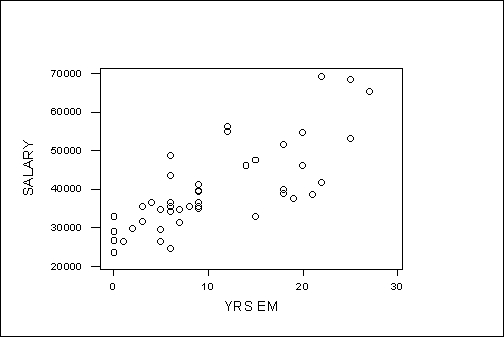
6.  ( 25 points).The plot below presents the scatter diagram of the variables:
      X: years of employment
      Y: salary
for 46 employees in the company Technitron in 1995.

The means and standard deviations of years of employment and salary and their covariance  are:

Mean of  "years of employment"   = 10.33

Standard deviation of "years of employment"  = 7.60

Mean of  "salary"  = $39,827

Standard deviation of  "salary" = $10,999

Covariance of "years of employment" and "salary" =  63,975

a)  What are the intercept and slope of the regression line of salary on years of employment?

b) What proportion of the total variability in salary is explainable by the linear regression of salary on years of employment?

c)   What is the predicted value of salary for a person having 10 years of employment?

d)  How much salary increase should an employee expect in one year?
 

Answers:
a) We have that b=Sx,y/Sx2 =63975/7.62=1,107.60 and

a=y(bar)-bx(bar)=39827-(1,107.60)(10.33)=$28,385.49

Intercept =$28,385.49
Slope =1,107.60 dollars/year

The regression line is y=28,385.49+1,107.60x.

b) Rxy=Sxy/SxSy= 63,975/(7.60)(10,999)=0.7653 is the correlation between salary and years of employement.
The proportion of the total variability in salary explainable by the linear regression is Rxy2 =0.5857

c)   Predicted salary in 10 years of employment is
y=a+bx =28,385.49+(1,107.60)(10)=$39,461.49

d)  The predicted salary increase in one year is $1,107.60

 
 

Comments to: Miguel A. Arcones