Splus has the following commands to do density estimation: hist, density,...
The command hist(x, nclass = , breaks = , plot = T, probability = F) allows to do count and probability histogram. It allows to obtain the points of the graph instead of the graph itself.
****** program 11a **********
# The data is the lengths of treatment spells in days of
# control patients in suicide study. The data is page 8 in
# Silverman (1986, Density Estimation for statistics and data analysis)
x_c(1,1,1,5,7,8,8,13,14,14,17,18,21,21,22,25,27,27,30,30,31,31,32,
+ 34,35,36,37,38,39,39,40,49,49,54,56,62,63,65,65,67,75,76,79,82,83,
+ 84,84,84,84,90,91,92,93,93,103,103,111,112,119,122,123,126,129,134,
+ 144,147,153,163,167,175,228,231,235,242,256,256,257,311,314,322,
+ 369,415,573,609,640,737)
y_c(0:8)*100
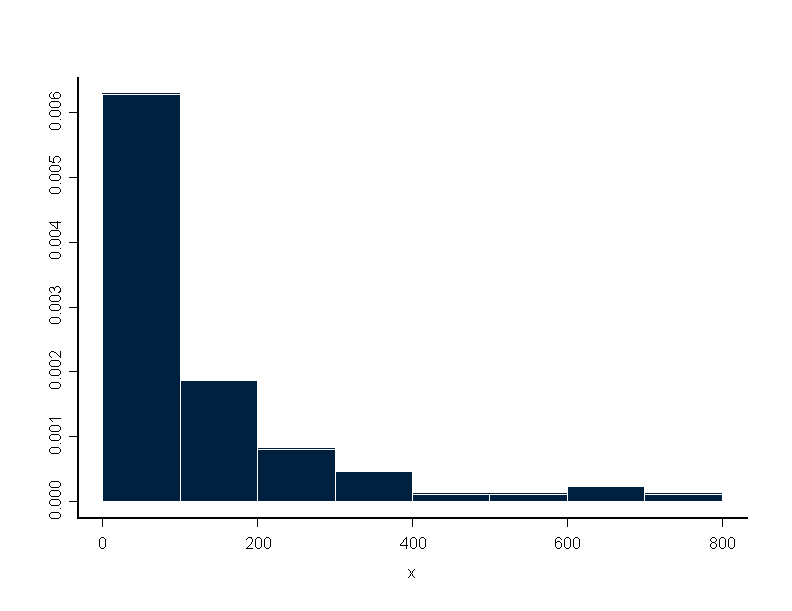
hist(x,breaks=y,plot=F,probability=T)
hist(x,breaks=y,plot=F,probability=F)
hist(x,breaks=y,probability=T)
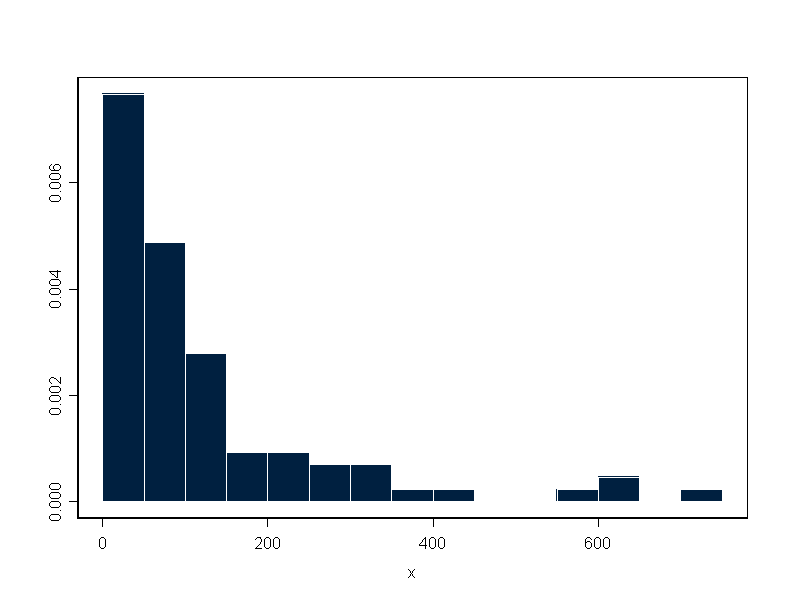
hist(x,nclass=15)
n_length(x)
h_50
x0_0
first_floor((min(x)-x0)/h)
last_ceiling((max(x)-x0)/h)
binmesh_ x0+h*c(first:last)
hist(x,breaks=binmesh,probability=T,plot=T)
box()
midpoints_x0+h*c(first-0.5:last+0.5)
res_list(midpoints)
names(res)_c("midp")
res
****** outcome ********** > hist(x, breaks = y, plot = F, probability = T) $breaks: [1] 0 100 200 300 400 500 600 700 800 $counts: [1] 0.0062790698 0.0018604651 0.0008139535 0.0004651163 [5] 0.0001162791 0.0001162791 0.0002325581 0.0001162791 > hist(x, breaks = y, plot = F, probability = F) $breaks: [1] 0 100 200 300 400 500 600 700 800 $counts: [1] 54 16 7 4 1 1 2 1

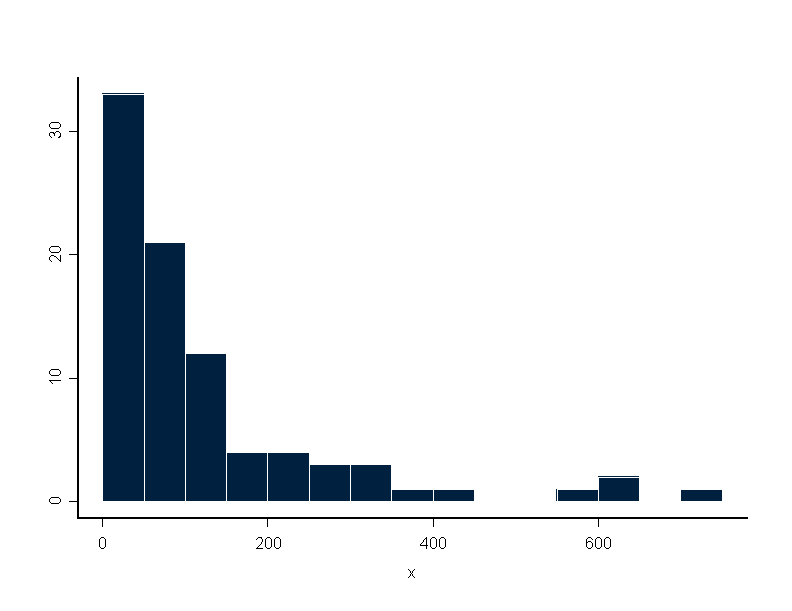
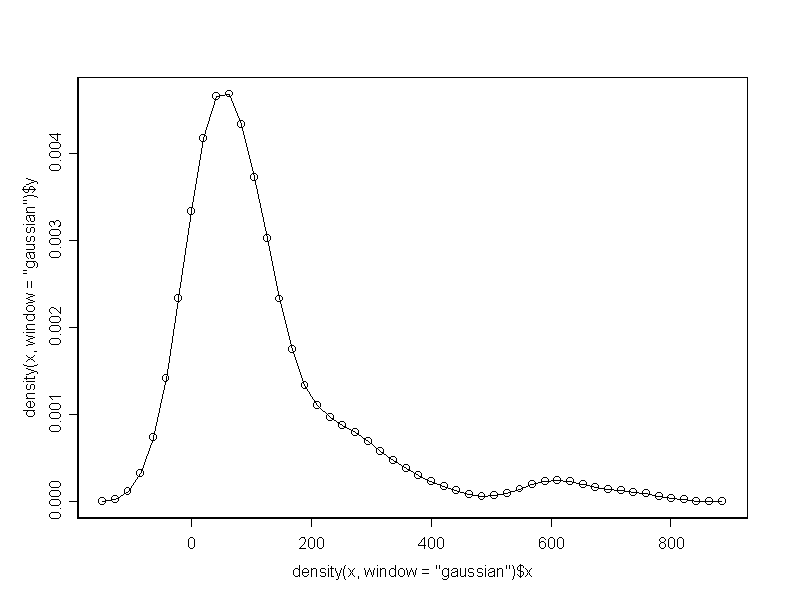
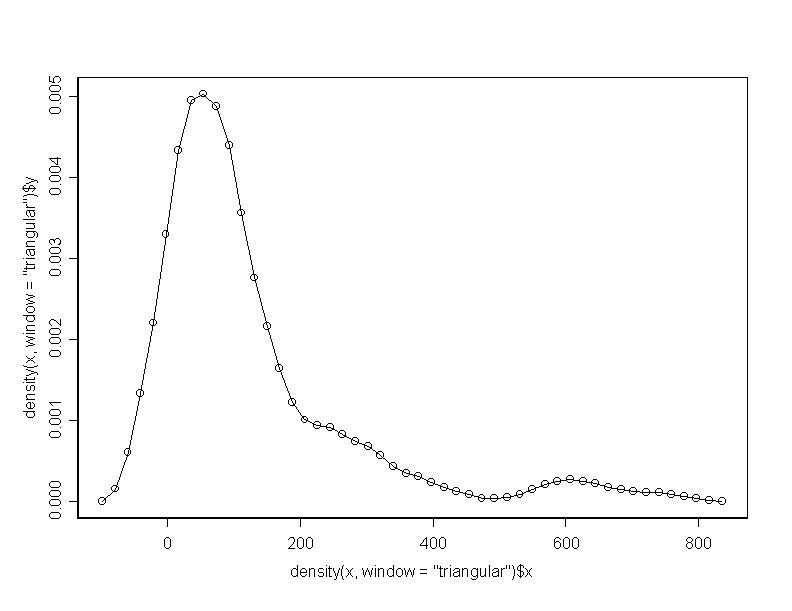
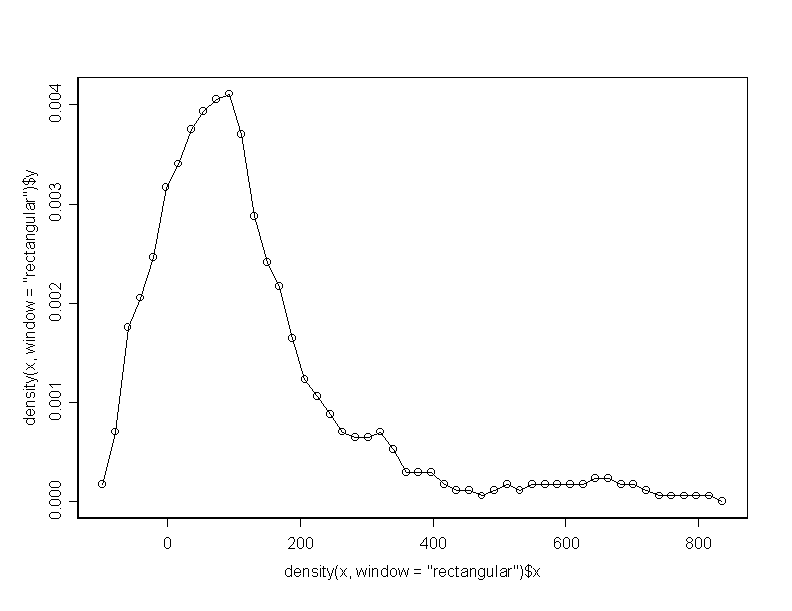
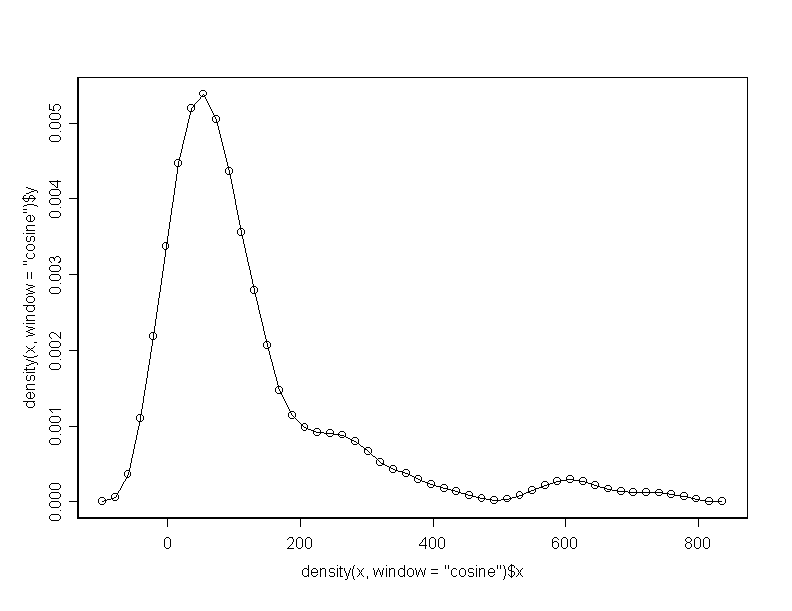
******* program 11b ************************************ density(x, window="gaussian") plot(density(x, window="gaussian")) lines(density(x,window="gaussian"),type="l") plot(density(x, window="triangular")) lines(density(x,window="triangular"),type="l") plot(density(x, window="rectangular")) lines(density(x,window="rectangular"),type="l") plot(density(x, window="cosine")) lines(density(x, window="cosine"),type="l")
> density(x, window = "gaussian") $x: [1] -147.66154608 -126.57331971 -105.48509333 [4] -84.39686696 -63.30864059 -42.22041422 [7] -21.13218785 -0.04396148 21.04426489 [10] 42.13249126 63.22071763 84.30894400 [13] 105.39717037 126.48539674 147.57362311 [16] 168.66184948 189.75007585 210.83830222 [19] 231.92652859 253.01475496 274.10298133 [22] 295.19120770 316.27943407 337.36766044 [25] 358.45588681 379.54411319 400.63233956 [28] 421.72056593 442.80879230 463.89701867 [31] 484.98524504 506.07347141 527.16169778 [34] 548.24992415 569.33815052 590.42637689 [37] 611.51460326 632.60282963 653.69105600 [40] 674.77928237 695.86750874 716.95573511 [43] 738.04396148 759.13218785 780.22041422 [46] 801.30864059 822.39686696 843.48509333 [49] 864.57331971 885.66154608 $y: [1] 3.127960e-006 3.133975e-005 1.223117e-004 [4] 3.263483e-004 7.406927e-004 1.421240e-003 [7] 2.339564e-003 3.338854e-003 4.179907e-003 [10] 4.655921e-003 4.687488e-003 4.333940e-003 [13] 3.729359e-003 3.022174e-003 2.332249e-003 [16] 1.752005e-003 1.339479e-003 1.102218e-003 [19] 9.702331e-004 8.814761e-004 7.932332e-004 [22] 6.898220e-004 5.791020e-004 4.763499e-004 [25] 3.846036e-004 3.046099e-004 2.359012e-004 [28] 1.752539e-004 1.248499e-004 8.384259e-005 [31] 6.416676e-005 7.037640e-005 9.945419e-005 [34] 1.465525e-004 1.956907e-004 2.338052e-004 [37] 2.464897e-004 2.323426e-004 2.006068e-004 [40] 1.663133e-004 1.407482e-004 1.247152e-004 [43] 1.102536e-004 9.016423e-005 6.587503e-005 [46] 4.043466e-005 2.126075e-005 9.327184e-006 [49] 3.414064e-006 0.000000e+000