First, we have X₁,...,X_m i.i.d.r.v.'s from the distribution function F. We want to estimate F by the empirical d.f. We want to find a band for F. We want to test Fo using the Kolmogorov-Smirnov test.

We can use the command cdf.compare in the one and two sample cases to graph distribution functions. For a one sample problem, compares the empirical distribution function (edf) of the sample with a hypothesized cumulative distribution function. For a two sample problem, compares the edfs for the two samples.

The command qqnorm(x) graphs the quantiles of the data versus the quantiles of a normal distribution. The formula for the quantiles of the normal distribution is PHI^-1((i-a)/(n+1-2*a)), where a=.5 if n>10 and a=.375 if n<=10. The command qqline(x) adds a line to the graph. To do other distributions, the command ppoints(n) returns p[i]=(i-a)/(n+1-2*a). This vector can be used to estimate the quantiles of a distribution. The to get the graph do: plot(qexp(ppoints(x)), sort(x)) (if using the exponential distribution). For two samples, the command qqplot(x,y) does a quantile-quantile plot for the data in x and y.

The command ks.gof(x, y) does a Kolmogorov-Smirmov test of fit in the one and two samples cases.

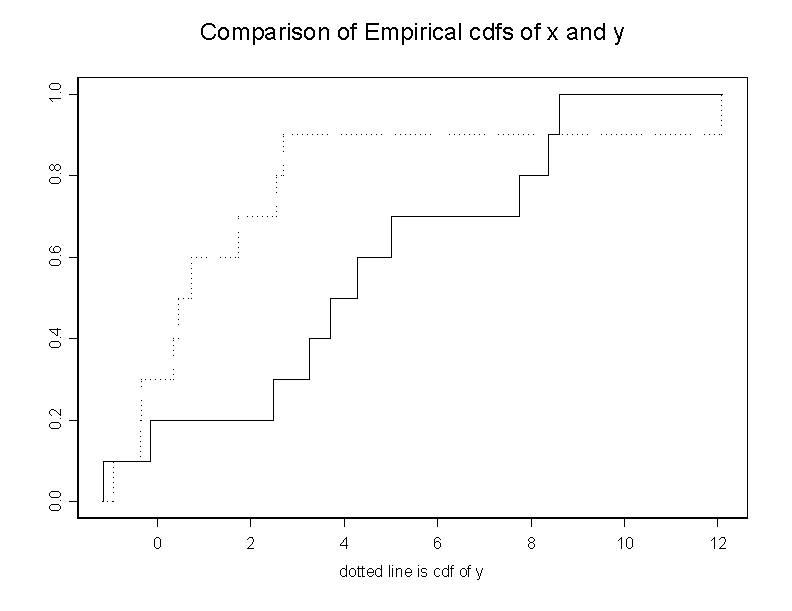
# Program 5b
# I take the data from  page 498 of the textbook.
# The following program does the following:
# 1. finds a confidence band for the distribution function.
# 2. draws the empirical d.f. and the df of a N(14,2) using cd.compare
# 3. qq plots; quantiles from the data with respect to the normal quantiles.
# 4. Kolmogorov-Smironov test for Fo=N(14,2) using ks.gof
# 5. Kolmogorov-Smironov test for Fo=N(14,2) directly.

#x_c(42,43,51,61,66,69,71,81,82,82)
x_c(12.8,12.9,13.3,13.4,13.7,13.8,14.5)
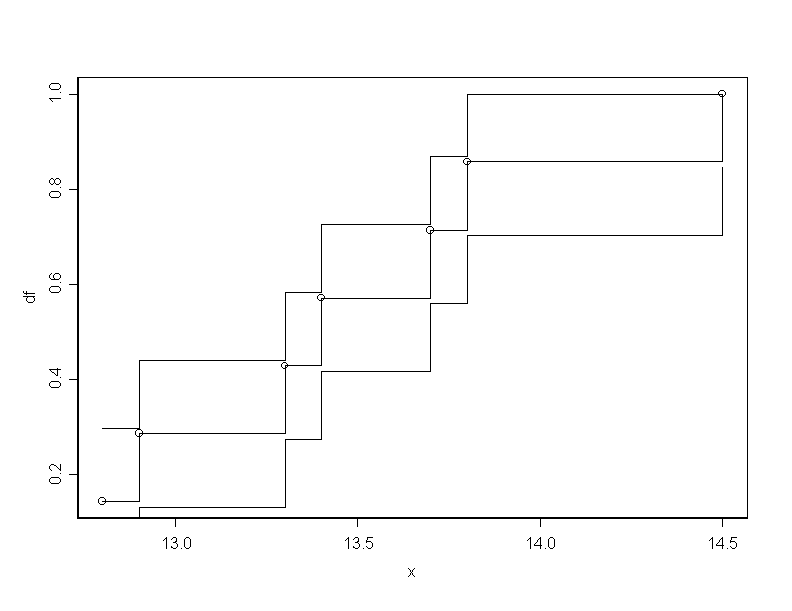
# First we find the confidence band for the df.
x.sort_sort(x)
n_length(x)
df_c(1:n)/n
dalpha_0.409
plot(x,df)
df1_(df-(dalpha/sqrt(n)))
df1_pmax(df1,0)
df2_(df+(dalpha/sqrt(n)))
df2_pmin(df2,1)
for(i in 1:n){
segments(x.sort[i], df[i], x.sort[i+1],df[i])
segments(x.sort[i], df[i-1], x.sort[i],df[i])
segments(x.sort[i], df1[i], x.sort[i+1],df1[i])
segments(x.sort[i], df1[i-1], x.sort[i],df1[i])
segments(x.sort[i], df2[i], x.sort[i+1],df2[i])
segments(x.sort[i], df2[i-1], x.sort[i],df2[i])
}
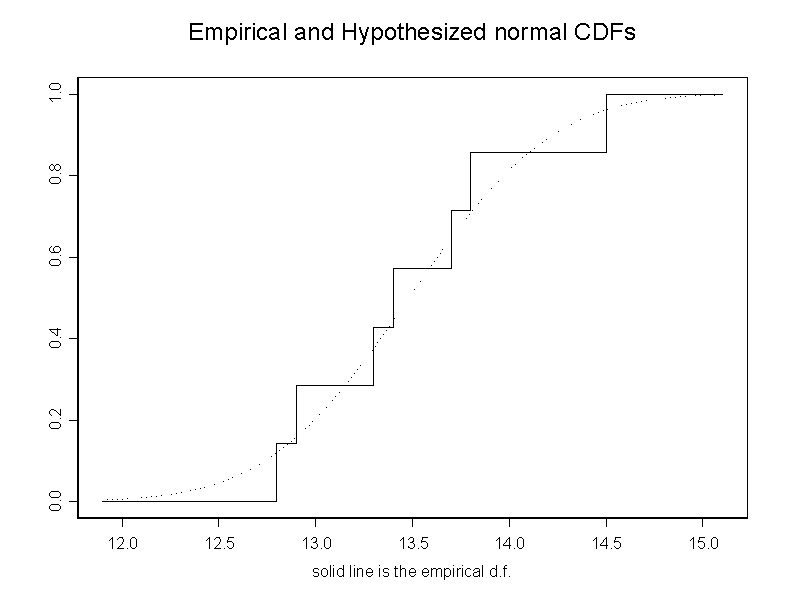
# the following command compares the df of x with the df of 
# normal r.v. with the parameters of x
cdf.compare(x, y = NULL, distribution = "normal",mean=mean(x),sd=stdev(x)) 
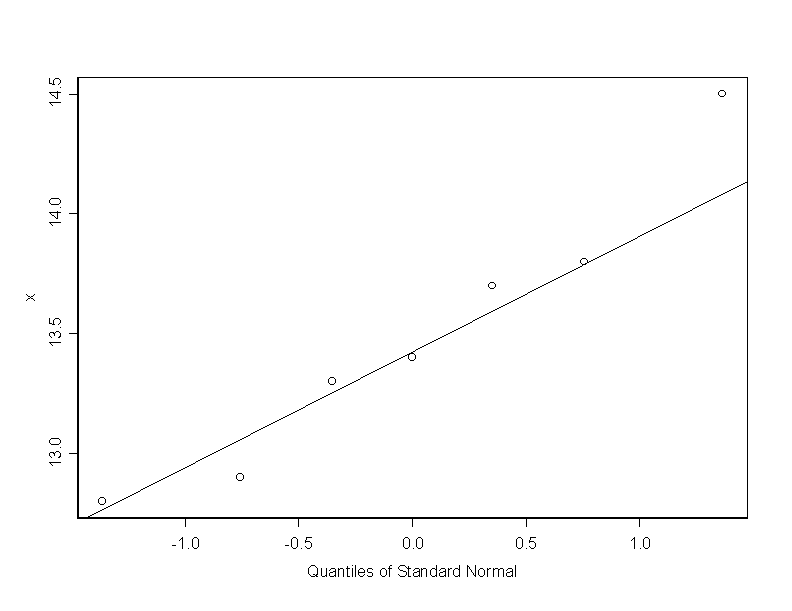
# next, we find the qq plot with respect to the normal quantiles
qqnorm(x)
qqline(x)
# we can do the Kolmogorov-Smirnov goodness of fitness test
ks.gof(x,y=NULL,alternative="two.sided",distribution="normal",mean=14,sd=2)
# we can find directly the Kolmogor-Smirnov statistic by doing:
x.sort_sort(x)
phi.x_pnorm(sort(x),mean=14,sd=2) 
n_length(x)
df_c(1:n)/n
a_max(abs(df-phi.x))
b_max(abs(phi.x+(1/n)-df))
kolmo_max(a,b)
print(kolmo)
N_10000
ks_c(1:N)
df_c(1:n)/n
for(i in 1:N){
xa_runif(n,0,1)	
xa_sort(xa) 
a_max(abs(df-xa))
b_max(abs(xa+(1/n)-df))
ks[i]_max(a,b)	
}
p.value.ks_sum(ks>kolmo)/N
print(p.value.ks)

The outcome of this program is

> ks.gof(x,y=NULL,alternative="two.sided",distribution="normal",m=14,sd=2)	
	# we can find directly the Kolmogor-Smirnov statistic by doing:

	One-sample Kolmogorov-Smirnov Test
	Hypothesized distribution = normal

data:  x 
ks = 0.4013, p-value = 0.1571 
alternative hypothesis: 
  True cdf is not the normal distn. with the specified parameters 

> print(kolmo)
[1] 0.4012937
> print(p.value.ks)
[1] 0.1544

We get a p-value very close to the one that Splus gives.

Here are the graphs.

The following program does the Lilliefort test for normality.

 
# program 5c
# We do the Lilliefort test of normality
# We use the data in  page 530 in the textbook. 
x_c(12.8,12.9,13.3,13.4,13.7,13.8,14.5)
n_length(x)
xa_sort(x)
xa_(xa-mean(xa))/stdev(xa)
phi.x_pnorm(xa)
df_c(1:n)/n
a_max(abs(df-phi.x))
b_max(abs(phi.x+(1/n)-df))
lilli_max(a,b)
print(lilli)
N_10000
lilli.sim_c(1:N)
for(i in 1:N){
x_rnorm(n)
xa_sort(x)
xa_(xa-mean(xa))/stdev(xa)
phi.x_pnorm(xa)
df_c(1:n)/n
a_max(abs(df-phi.x))
b_max(abs(phi.x+(1/n)-df))
lilli_max(a,b)
lilli.sim[i]_max(a,b)	
}
p.value.lilli_sum(lilli.sim>lilli)/N
print(p.value.lilli)

The outcome of this program is

> print(p.value.lilli)
[1] 0.267

The following program does a Shapiro-Wilks test of normality.

# program 5d
# We do the Wilks-Shapiro test of normality
# We use the data in  page 530 in the textbook. 
x_c(12.8,12.9,13.3,13.4,13.7,13.8,14.5)
n_length(x)
xa_sort(x)
xa_xa-mean(xa)
phi_c(1:n)
phi_pnorm((phi-(1/2))/n)
corr_cor(xa,phi)
N_10000
sw_c(1:N)
corr.sim_c(1:N)
for(i in 1:N){
x2_rnorm(n)
x2a_sort(x2)
x2a_x2a-mean(x2a)
phi_c(1:n)
phi_pnorm((phi-(1/2))/n)
corr.sim[i]_cor(x2a,phi)	
}
print(summary(corr.sim))
p.value.sw_sum(corr < corr.sim)/N
print(corr)
print(p.value.sw)

The outcome of the program is:

> print(p.value.sw)
[1] 0.5444

Observe how different the two p-values are using the different methods. This happens because the number of observations n=7 is too small to do tests of normality.

This is program for the two samples case:

# program 5e
# I use the data in the Table 5.7, page 180 from the textbook.
# We want to compare the two df's
# We get the following:
# 1. A graph with the two df's.
# 2. The Kolmogorov-Smirnov test
# 3. The qqplot.
#
x_c(-.15,8.6,5.,3.71,4.29,7.74,2.48,3.25,-1.15,8.38)
y_c(2.55,12.07,.46,.35,2.69,-.94,1.73,.73,-.35,-.37)
cdf.compare(x,y)
ks.gof(x,y)
qqplot(x,y)

The outcome of the program is

> ks.gof(x, y)

	Two-Sample Kolmogorov-Smirnov Test

data:  x and y 
ks = 0.6, p-value = 0.0524 
alternative hypothesis: 
  cdf of x does not equal the
              cdf of y for at least one sample point. 

Here are the graphs.

Comments to: Miguel A. Arcones