Top



Next: About this document
- In a randomized controlled experiment,
- the control group always gets a placebo.
- the subjects randomly assign themselves to the treatment and control groups.
- the treatment group is similar to the control group, apart from the treatment.
- (a), (b) and (c) are all true.
- none of the above are true.
- In an observational study,
- the control group always gets a placebo.
- the experimenter randomly assigns the subjects to the treatment and control groups.
- the treatment group is similar to the control group, apart from the treatment.
- an association between two things can be established.
- none of the above are true.
- In a double blind experiment,
- a placebo is not necessary.
- neither the subjects nor the people who evaluate the responses actually know who got the treatment.
- only the people who evaluate the responses know who got the treatment.
- both (a) and (b) are true.
- both (a) and (c) are true.
- Confounding with unrelated factors can be a serious problem in
- controlled experiments.
- randomized controlled experiments.
- observational studies.
- both (a) and (c).
- both (b) and (c).
- Which of the following is a qualitative measurement?
- GPA (grade point average).
- Hair color.
- Weekly income.
- Both (a) and (c) are qualitative measurements.
- None of the above are qualitative measurements.
- In a series of repeated measurements, bias
- changes from measurement to measurement, sometimes up and sometimes down.
- does not affect the long run average of repeated measurements.
- can easily be detected just by looking at the measurements.
- satisfies both (a) and (b).
- satisfies none of the above statements.
- When data is collected from a series of repeated measurements,
- both the average and the standard deviation of the data are strongly influenced by outliers in the data.
- chance error changes from measurement to measurement; bias does not.
- the likely size of the chance error can be estimated by the SD of the sequence of measurements.
- both (b) and (c) are true.
- all of the above statements are true.
- A histogram
- represents percents by area.
- consists of a set of blocks where the area of each block equals the percentage of cases in the corresponding class interval.
- of quantitative data always has about 68% of the observations within 1 SD of the average.
- satisfies both (a) and (b).
- satisfies all of the above.
- For a list of observations following a normal curve,
- about 95% of the observations are within 2 SDs of the average.
- about 50% of the observations are less than the median.
- converting an observation into standard units tells how many SDs it is above (+) or below (-) the average.
- both (a) and (c) are true.
- all of the above statements are true.
- The correlation coefficient between two variables
- is not affected by outliers.
- is always between 0 and 1.
- is 0 when there is tight clustering of the points around the SD line.
- is a measure of the linear association between the two variables.
- satisfies all of the above.
- Which one of the following statements is true?
- If 3.5 is the 25th percentile of a set of data then the interquartile range for the data must be 7.
- The standard deviation of a set of data can never be zero.
- The slope of a straight line is equal to run/rise.
- If there is a strong association between two variables then the correlation coefficient must be close to one.
- None of the statements (a) - (d) are true.
- In a completely randomized design,
- the subjects assign themselves to the treatment and control groups.
- the investigators use their best judgement to assign the subjects to the treatment and control groups.
- historical controls may sometimes be used if the investigators have good reason for doing so.
- there is a serious possibility of confounding with unknown factors.
- none of the above are true.
- In an observational study,
- confounding is a potential problem.
- a placebo must always be used.
- the subjects are assigned at random by the investigators to the treatment and control groups.
- the investigators use their best judgement to assign the subjects to the treatment and control groups.
- confounding is not a potential problem.
- A qualitative variable is one which
- generally takes on numerical values.
- generally does not take on numerical values.
- generally takes on discrete numerical values.
- is never used in statistical studies.
- satisfies both (b) and (d) above.
- An outlier
- has no effect on the standard deviation of a variable.
- is an observation with an extreme value
- is caused by confounding of variables in the experiment.
- has no effect on the average of a variable.
- always means that there is an error in recording experimental data.
- Bias in statistical measurements
- generally varies from measurement to measurement.
- is caused by random measurement errors.
- is a systematic error in all measurements and effects all measurements the same way.
- can generally be ignored because of its random nature.
- can be readily detected by looking at the measurements themselves.
- In a double blind experiment,
- a control group is not necessary.
- neither the subjects nor the people who evaluate the responses actually know who got the treatment.
- only the subjects know who got the treatment.
- the possibility of bias is increased.
- both (a) and (b) are true.
- In a completely randomized experiment,
- the treatment group is similar to the control group, apart from the treatment.
- the treatment group always gets a placebo.
- the subjects always know which group they belong to.
- there is a serious possibility of confounding with unknown factors.
- none of the above are true.
- In an observational study,
- the control group always gets a placebo.
- the subjects choose which group they belong to.
- the treatment group is similar to the control group, apart from the treatment.
- confounding is not a potential problem.
- none of the above are true.
- A confounding factor
- can never be controlled for in an observational experiment.
- always increases the standard deviation of the data.
- may cause the results of an experiment to be misinterpreted.
- satisfies both (a) and (b).
- satisfies both (b) and (c).
- Confounding with unrelated factors can be a serious problem in
- randomized controlled experiments.
- controlled experiments.
- observational studies.
- both (a) and (c).
- both (b) and (c).
- In a series of repeated measurements, bias
- generally varies from measurement to measurement, sometimes up and sometimes down.
- is a systematic error in all measurements and affects all measurements the same way.
- can generally be ignored because of its random nature.
- can be readily detected by looking at the measurements themselves.
- satisfies both (a) and (c).
- When data is collected from a series of repeated measurements,
- both the median and the standard deviation of the data are strongly affected by outliers in the data.
- the median is used as a numeric measure of the spread of the data.
- the standard deviation of the data can be used to estimate the bias in the measurements.
- chance error in the measurements affects all measurements the same way.
- none of the above statements are true.
- A histogram
- is a graph which is used to summarize data.
- represents percents by area.
- consists of a set of blocks where the height of each block equals the percentage of cases in the corresponding class interval.
- satisfies both (a) and (b).
- satisfies all of the above.
- When the histogram of a set of data follows the normal curve,
- about 68% of the data is within one standard deviation (SD) of the average.
- about 90% of the data is within two SDs of the average.
- about 95% of the data is within two SDs of the average.
- both (a) and (b) are true.
- both (a) and (c) are true.
- Which one of the following statements (a) - (d) is not true?
- If 3.5 is the 25th percentile of a set of data then the interquartile range for the data must be 7.
- The standard deviation of a set of data can never be negative.
- The normal curve is symmetric about zero.
- The 50th percentile of a set of data is the same as the median of the data.
- All of the above statements are true.
- For a straight line plotted on an x-y graph,
- the slope equals rise/run.
- the slope equals run/rise.
- the intercept is where the line crosses the x- axis.
- both (a) and (c) are true.
- both (b) and (c) are true.
- The correlation coefficient
- measures association in a scatter plot.
- always lies between 0 and 1.
- implies causation if its value is close to 1.
- is used to determine the slope of the SD line.
- satisfies none of the above.
- The correlation coefficient
- is not affected by outliers.
- has the property that a value of -1 indicates the weakest possible association and a value of +1 indicates the strongest possible association.
- is reliable if the scatter plot consists of two completely separate clusters.
- is a good measure of nonlinear association.
- satisfies none of the above.
- In a regression setting for predicting y from x,
- the R.M.S. error is generally smaller than the SD of y.
- the R.M.S. error is generally smaller than the SD of x.
- the R.M.S. error is generally larger than the SD of y.
- the R.M.S. error is generally larger than the SD of x.
- both (a) and (b) are true.
- In a regression setting for predicting y from x,
- the regression line for the residual plot is vertical.
- the average of the residual values is 1.
- the residuals should show a strong pattern if the analysis is to be reliable.
- the average of the residual values is 0.
- both (c) and (d) are true.
- Heteroscedasticity in a regression setup
- makes the R.M.S. error more reliable.
- makes the prediction error more uniform.
- means that the scatter diagram has a generally elliptical (football) shape.
- means that the scatter diagram does not have an elliptical shape.
- both (a) and (c) are true.
- When summarizing the relationship between two variables x and y
- the average of the x values is needed.
- the average of the y values is needed.
- the SD of the x values is needed.
- the SD of the y values is needed.
- the correlation coefficient is needed.
- all of the above are true.
- The following is not a property of Chance (or probability),
- Chance lies between 0% and 100%.
- The chance of an event is 100% minus the chance of the opposite event.
- The chance of at least one of two events happening is always the sum of the chances of the separate events.
- If two events are independent, the chance that both will happen equals the product of chances of the separate events.
- Chance can be thought of as the percent of the time that an event occurs when the basic process is repeated over and over.
- For two mutually exclusive events
- the probability of both events occurring is the product of the individual probabilities.
- the probability of both events occurring is the sum of the individual probabilities.
- the probability of both events occurring is 1.
- the probability of both events occurring is 0.
- none of the above are true.
- The event A has a 40% chance of happening. The event B has a 60% chance of happening. If the chance that both events happen together is 24% then
- the two events are mutually exclusive.
- the two events are independent.
- the two events are dependent.
- both (a) and (b) are true.
- no conclusion can be drawn because there isn't enough information.
- The event A has a 30% chance of happening. The event B has a 60% chance of happening. If the chance that at least one of the events happens is 80% then
- the two events are not mutually exclusive.
- the two events are mutually exclusive.
- the two events are independent.
- the regression line between the events is not linear.
- none of the above is true.
- If there is a strong association between two variables, then
- there is a cause and effect relationship between the variables.
- the correlation coefficient must be close to one.
- knowing one variable helps a lot in predicting the other.
- both (b) and (c) are true.
- all of the above statements are true.
- In a regression setting for predicting y from x,
- the r.m.s. error can be calculated as
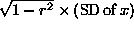 .
.
- the units for the r.m.s. error are the same as the units for the variable being predicted.
- if a regression is appropriate for the data, then the residual plot should show a heteroscedastic pattern.
- both (b) and (c) are true.
- all of the above statements are true.
- In virtually all test-retest situations,
- the bottom group on the first test will on average show some improvement on the second test.
- the top group on the first test will on average show some improvement on the second test.
- the regression fallacy consists in thinking that the regression effect shown in the exam scores on the two tests must be due to the spread of the data around the SD line.
- both (a) and (b) are true.
- all of the above statements are true.
- In a regression setting for predicting y from x, the regression line and the SD line are the same
- if the correlation coefficient is 0.
- if the correlation coefficient is -1.
- if the SD of y-values equals the SD of the x-values.
- if the average of the y-values equals the average of the x-values.
- if both (c) and (d) hold true for the data.
- If the correlation coefficient between two variables is zero (r = 0), then
- the scatter plot of the two variables shows no pattern whatsoever.
- none of the points on the scatter plot lie within 1 SD of the regression line.
- there is a tight clustering about the SD line.
- there is no linear association between the variables.
- all of the above statements are true.
- The correlation coefficient between two variables
- is affected by interchanging the variables.
- is affected by multiplying all of the values of one variable by the same positive number.
- is affected by adding the same number to all of the values of one variable.
- is affected by multiplying all of the values of one variable by the same negative number.
- always lies between 0 and 1.
- In a regression setting for predicting y from x,
- the regression line is just a smoothed version of the graph of averages.
- the regression line passes through the point of averages.
- the r.m.s. error measures the deviation of the scatter diagram's points from the SD line.
- both (a) and (b) are true.
- all of the above statements are true.
- If A and B are independent events,
- the chance that A happens given that B happened is the same as the chance that B happens.
- the two events A and B must be mutually exclusive.
- the chance of A and B both happening is equal to the chance of A plus the chance of B.
- both (b) and (c) are true.
- none of the above statements are true.
- For two mutually exclusive events,
- the probability that at least one of the events occurs is the sum of the individual probabilities.
- the probability that at least one of the events occurs is the product of the individual probabilities.
- the probability that both of the events occur is the sum of the individual probabilities.
- the probability that both of the events occur is the product of the individual probabilities.
- none of the above statements are true.
- The event A has a 30% chance of happening. The event B has a 60% chance of happening. If the chance that both events happen together is 18% then
- the two events are mutually exclusive.
- the two events are dependent.
- the chance that A happens given that B happens is 30%.
- the chance that A happens given that B happens is 18%.
- both (a) and (b) are true.
- When drawing tickets at random with replacement from a box,
- the draws are independent.
- the draws are mutually exclusive.
- the draws are dependent.
- both (a) and (b) are true.
- both (b) and (c) are true.
- Under certain requirements the binomial formula,
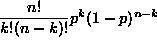 , can be used to calculate the chance that an event occurs exactly k times in n trials. Which of the following is not one of the requirements for using the binomial formula?
, can be used to calculate the chance that an event occurs exactly k times in n trials. Which of the following is not one of the requirements for using the binomial formula?
- The trials must be independent.
- The value of n must be fixed in advance.
- The value of p must be the probability that the event will occur on any particular trial.
- The value of p cannot change from trial to trial.
- All of the above requirements are needed to use the binomial formula.
- The binomial formula can be used to calculate
- the probability of getting exactly 3 heads in 10 tosses of a coin.
- the probability of getting exactly 3 aces before getting a six when rolling a fair die.
- the probability of having exactly 3 red cards among the top 10 cards in a well shuffled standard deck of cards.
- both (a) and (b).
- both (a) and (c).
- When tossing a fair coin and counting the number of heads obtained, the number of heads equals half the number of tosses plus a chance error. The law of averages says that
- the chance error is small if the number of tosses is large.
- the chance of getting 50 heads out of 100 tosses is the same as getting 500 heads out of 1000 tosses.
- the number of heads equals half the number of tosses if the number of tosses is large.
- the percentage of heads is likely to be close to 50% if the number of tosses is large.
- both (a) and (d) are true.
- Which of the following is not a property of probability histograms?
- A probability histogram represents chance by area.
- The total area under a probability histogram is 100%.
- A probability histogram represents data obtained from a sample.
- A probability histogram always follows the normal curve.
- Both (c) and (d) are not properties of probability histograms.
- Draws are made at random with replacement from a box, and the number of draws is getting larger and larger. Which of the following statements is not true?
- The probability histogram for the sum (when put in standard units) follows the normal curve more and more closely.
- The histogram for the numbers drawn follows the probability histogram for the numbers in the box more and more closely.
- The histogram for the contents of the box (when put in standard units) follows the normal curve more and more closely.
- The probability histogram for the numbers in the box remains the same.
- The expected value of the sum locates the center of the probability histogram for the sum.
- A fair coin is tossed 100 times landing heads 53 times. The last 9 tosses of the coin were all heads. Which of the following best characterizes what will happen if the coin is tossed one more time?
- The chance of getting a head is greater than 50%.
- The chance of getting a head is less than 50%.
- The chance of getting a head is exactly 50%.
- The chance of getting a head is exactly 53%.
- Both (a) and (d) are true.
- When sampling from a population, which of the following is generally not true?
- The method of choosing a sample matters a lot regardless of the sample size.
- The best methods of choosing a sample are probability methods which involve an objective chance process to pick the sample.
- The parameters are estimated by statistics which are numbers computed from the sample.
- The larger the population is the larger the sample size should be.
- Sampling is used because it is impractical to study the entire population.
- The Literary Digest poll of the 1936 presidential election
- was an example of an excellent sampling procedure.
- was the first poll to accurately predict the next president of the United States.
- had a very low non-response rate.
- was an example of a biased sampling procedure.
- satisfied items (a), (b) and (c).
- When sampling from a population, which of the following is true?
- Non-response bias is not important.
- Non-response bias is important but can be overcome by increasing the sample size.
- Selection bias is not important.
- Selection bias is important and cannot be overcome by increasing the sample size.
- Selection bias is important but can be overcome by increasing the sample size.
- Simple random sampling
- means drawing at random with replacement.
- is very similar to quota sampling.
- means drawing at random without replacement.
- introduces selection bias.
- both (c) and (d) are true.
- In a simple random sample the difference between a sample percentage and a population percentage is
- due to sample selection bias, the size of which cannot be estimated.
- due to sample selection bias, the size of which can be estimated by the SE.
- due to chance error, the size of which cannot be estimated.
- due to chance error, the size of which can be estimated by the SE.
- explained by (a) and (d) combined.
- When estimating a population percentage from a sample,
- the absolute size of the sample determines the accuracy of the estimate.
- a correction factor is never needed if the sample is a simple random sample.
- doubling the sample size makes the SE increase by a factor of 2.
- doubling the sample size makes the SE decrease by a factor of 2.
- the size of the sample relative to the population determines the accuracy of the estimate.
- Both (a) and (e) are true.
- Under certain requirements the binomial formula,
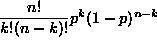 , can be used to calculate the chance that an event occurs exactly k times in n trials. Which of the statements (a) - (d) is not one of the requirements for using the binomial formula?
, can be used to calculate the chance that an event occurs exactly k times in n trials. Which of the statements (a) - (d) is not one of the requirements for using the binomial formula?
- The trials must be dependent.
- The value of n must be fixed in advance.
- The value of p must be the probability that the event will occur on any particular trial.
- The value of p cannot change from trial to trial.
- All of the above requirements are needed to use the binomial formula.
- A single die is rolled five times. We wish to use the binomial formula to calculate the probability that exactly two of the rolls had a three showing. In this case
- the correct value for n is 2.
- the correct value for p is 1/2.
- the correct value for k is 2.
- both (b) and (c) are true.
- it is improper to use the binomial formula.
- When tossing a fair coin and counting the number of heads obtained, the law of averages states that
- the number of heads equals the number of tosses plus a chance error.
- the number of heads equals half the number of tosses if the number of tosses is large.
- the percentage of heads equals 50% if the number of tosses is large.
- both (a) and (c) are true.
- none of the above are true.
- When drawing one hundred numbered tickets at random with replacement from a box,
- the sum of the tickets is equal to the expected value for the sum of the draws plus a chance error, where the size of the chance error is given by the SD of the box.
- the expected value for the sum of the draws is given by
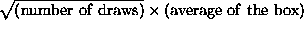 .
.
- the SE of the box is given by
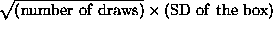 .
.
- all of the above are true.
- none of the above are true.
- A probability histogram
- represents chance by area.
- is the same thing as an empirical histogram.
- must be based on a large number of observations.
- always follows the normal curve.
- satisfies both (a) and (d).
- Draws are made at random with replacement from a box. Which of the following statements is true?
- The histogram for the contents of the box (when put in standard units) follows the normal curve if the number of draws is large.
- The probability histogram for the sum (when put in standard units) follows the normal curve if the number of draws is large.
- The probability histogram for the sum (when put in standard units) always follows the normal curve regardless of the number of draws.
- The probability histogram for the sum (when put in standard units) follows the normal curve when the number of draws is large only if the contents of the box also follow a normal curve.
- Statements (a) and (b) are both true.
- Here are two situations: (1) A fair coin is tossed 100 times and the percentage of heads is recorded. (2) A fair coin is tossed 1000 times and the percentage of heads is recorded. Which of the following statements is true?
- The chance of getting between 45% and 55% heads is greater in situation (1) than it is in situation (2).
- The chance of getting between 45% and 55% heads is greater in situation (2) than it is in situation (1).
- The chance of getting less than 45% heads is greater in situation (1) than it is in situation (2).
- Both (a) and (c) are true.
- Both (b) and (c) are true.
- When sampling from a population, if a biased selection procedure is used
- the bias can be reduced by increasing the sample size.
- the bias is the chance error which varies from individual to individual.
- the bias is unimportant if the SE of the sample is small.
- both (a) and (c) are true.
- none of the above are true.
- The Literary Digest poll of the 1936 presidential election
- was the first poll to accurately predict the next president of the United States.
- suffered from non-response bias.
- suffered from selection bias.
- suffered from both selection bias and non-response bias.
- satisfies none of the above.
- In a simple random sample, increasing the sample size by a factor of four
- decreases the SE for a percentage by a factor of four.
- decreases the SE for the sum by a factor of four.
- decreases the SE for a percentage by a factor of two.
- decreases the SE for the sum by a factor of two.
- both (c) and (d) are true.
- When estimating a population percentage from a sample,
- a large population needs a larger sample size than a small population to obtain the same level of accuracy of the estimate.
- a correction factor is never needed if the sample is a simple random sample.
- the accuracy of the estimate does not depend on the sample size.
- if the sample is a large part of the population then the estimate is likely to be unreliable.
- none of the above are true.
- Among all applicants to a certain university one year, the math SAT scores averaged 535, the SD was 100, and the scores followed the normal curve. One applicant scored 710 on the math SAT. What was her percentile rank (among all the applicants)?
- Her percentile rank was 80%.
- Her percentile rank was 84%.
- Her percentile rank was 92%.
- Her percentile rank was 96%.
- Her percentile rank was 98%.
- In an observational study,
- the investigators always assign the subjects to the treatment and control groups.
- the subjects are randomly assigned to the treatment and control groups.
- a placebo must always be used for the control group.
- confounding is a potential problem.
- both (a) and (c) are true.
- When performing repeated measurements using the same process, the bias
- generally changes from measurement to measurement.
- is a systematic error in all measurements and effects all measurements the same way.
- is caused by random measurement errors.
- can be readily detected by looking at the measurements themselves.
- satisfies both (a) and (b) above.
- When studying the relationship between two variables, the correlation coefficient
- has the property that a value of -1 indicates the weakest possible association and a value of +1 indicates the strongest possible association.
- measures linear association in a scatter plot of the two variables.
- always lies between 0 and 1.
- is used to determine the slope of the SD line for the variables.
- satisfies none of the above.
- Homoscedasticity in a regression setup
- makes the R.M.S. error very unreliable.
- means that the regression effect is due to something other than the spread around the SD line.
- means that the scatter diagram has a generally elliptical (football) shape.
- means that the scatter diagram does not have an elliptical shape.
- both (a) and (d) are true.
- A random sample of 10,000 voters is taken and classified according to income status and political party affiliation. The following table summarizes the observations:
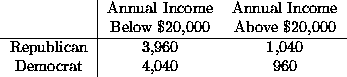
To test the null hypothesis that the percentage of voters who are Republicans and who have annual incomes exceeding $20,000 is 10%, against the alternative hypothesis that the percentage is greater than 10% the following test of significance should be used.
- A z-test using the normal curve.
- A two sample z-test for the difference in percentages.
- A t-test using Student's curve with 1 degree of freedom.
- A
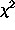 -test (chi-squared test) with one degree of freedom.
-test (chi-squared test) with one degree of freedom.
- None of the above tests should be used.
- When drawing at random with replacement from a box of tickets, increasing the sample size (number of draws) by a factor of 4
- multiplies the SE for the average by a factor of 4.
- divides the SE for the average by a factor of 4.
- multiplies the SE for the average by a factor of
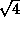 .
.
- divides the SE for the average by a factor of
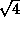 .
.
- has no effect at all on the SE for the average.
- Which one of the following statements about the Gauss model for measurement error is not true?
- The average of the error box is zero.
- The actual measurement is the exact value plus a chance error.
- When estimating the exact value, repeated measurements will not improve the overall accuracy of the estimate.
- The SD of many repeated measurements can be used to estimate the SD of the error box.
- The chance variability is in the measuring process, not the thing being measured.
- Which of the following is not needed to compute a confidence interval for the population average?
- The sample size.
- The confidence level.
- The sample average.
- The sample SD.
- All of the above are needed to compute a confidence interval for the population average.
- When performing a test of significance a box model is set up, the null and alternative hypotheses are formulated and
- the Student's curve is used when the SD of the box is known.
- the Student's curve is used when the histogram of the box is quite different from the normal curve.
- the Student's curve is used when the number of measurements (draws from the box) is less than 25 and the histogram of the box is not too different from a normal curve.
- the Student's curve is used when the number of measurements (draws from the box) is very large but the histogram is quite different from the normal curve.
- both (a) and (d) are true.
- When calculating the standard error from a box model which one of the following statements is not true?
- SE for sum =
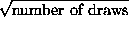 x SD of box.
x SD of box.
- SE for average =
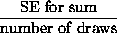 .
.
- SE for average =
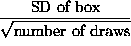 .
.
- SE for percent =
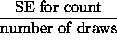 x 100%, where SE for count = SE for sum from a 0 - 1 box.
x 100%, where SE for count = SE for sum from a 0 - 1 box.
- All of the above statements are true.
- When performing a test of significance,
- the P-value gives the chance that the null hypothesis is true.
- the larger the P-value the more evidence there is that the alternative hypothesis is true.
- if the P-value is less than 1% then the result is not significant.
- the P-value is computed assuming the null hypothesis is true.
- both (a) and (b) are true.
- When drawing tickets at random with replacement from a box, the SD of the box can be estimated by
- using the SE of the sample average to estimate the SD of the box.
- using the sample average to estimate the SD of the box.
- using the SD of the sample to estimate the SD of the box.
- using the SE for the sum of the draws to estimate the SD of the box.
- none of the above methods.
- Which one of the following statements about histograms is not true?
- If a histogram for data has a long right tail then the median for the data is less than the average of the data.
- If two lists of data have exactly the same average and the same SD then their histograms must also be the same.
- A histogram represents percents by area.
- Half of the area of a histogram is to the left of the median.
- All of the above statements are true.
- A simple random sample of size 25 is drawn (without replacement) from a population of size 100. Which one of the following statements describes the correction factor needed for the SE of the average?
- The correction factor is about .25.
- The correction factor is about .76.
- The correction factor is about .87.
- The correction factor is about .99.
- No correction factor is needed for the SE of the average.
- To test a genetic model, an experimenter sets up a null hypothesis and a one sided alternative hypothesis, collects data and computes the z-statistic. A z-statistic of zero would be expected according to the null hypothesis. The experimenter obtains a z-statistic of 1.65. Which of the following statements is true?
- The observed level of significance (P-value) is about 5%.
- The chance the model is correct is about 95%.
- The chance the model is correct is about 5%.
- The chance of getting results this extreme is about 95%.
- The chance of getting results this extreme is about 5%.
- Which of the following statements is true?
- If a histogram for data has a long right tail then the median for the data is greater than the average of the data.
- In an observational study confounding is a potential problem.
- An outlier has no effect on the average of a variable.
- Both (a) and (b) are true.
- None of the above are true.
- Heteroscedasticity in a regression setup
- means that the regression effect is due to something other than the spread around the SD line.
- means that the scatter diagram has a generally elliptical (football) shape.
- means that the scatter diagram does not have an elliptical shape.
- always makes the R.M.S. error very small.
- both (b) and (d) are true.
- When studying the relationship between two variables, the correlation coefficient
- has the property that a value of -1 indicates the weakest possible association and a value of +1 indicates the strongest possible association.
- measures the linear association in a scatter plot of the two variables.
- is used to determine the slope of the SD line for the variables.
- satisfies both (a) and (b) above.
- satisfies none of the above.
- The binomial formula can be used to calculate
- the probability of getting exactly 4 heads in 10 tosses of a coin.
- the probability of getting exactly 4 heads before getting a tail when tossing a fair coin.
- the probability of having exactly 4 black cards among the top 10 cards in a well shuffled standard deck of cards.
- both (a) and (b).
- both (a) and (c).
- A percentage obtained from a simple random sample
- has an expected value equal to the population percentage.
- has an SE equal to the population SD.
- has an SE equal to the population SD divided by the population size.
- satisfies both (a) and (c) above.
- satisfies none of the above.
- When drawing a sample from a box for which the SD is unknown, a reasonable estimate for the SE of the average of the sample is
- the SD of the sample divided by the sample size.
- the SD of the sample divided by the square root of the sample size.
- the SD of the sample multiplied by the square root of the sample size.
- the SD of the sample multiplied by the sample size.
- not possible to estimate since there is no reasonable way to estimate the SE of the average without knowing the SD of the box.
- In the model for measurement error presented in the text,
- when the Gauss model applies the SD of a series of repeated measurements can be used to estimate the SD of the error box.
- when the Gauss model applies, the SD of the error box is always known.
- when the Gauss model applies, any bias in the measurements can be easily detected.
- the Gauss model can be written as: exact value = exact value + bias + chance error.
- both (b) and (c) are true.
- In Mendel's study of genetics,
- his data did not fit his theory very well, just barely supporting his claims.
- his data did fit his theory very well, almost too good to be true.
- his data fit his theory in a way which is to be expected, neither too well nor too poorly.
- he didn't even use data to support his theory.
- none of the above statements is true.
- When calculating the SE for the sum of draws from a box, the correction factor
- is used only when the draws are made with replacement.
- is always a number that is less than one.
- is used only when the number of draws from the box is very small compared to the number of tickets in the box and the draws are made without replacement.
- satisfies all of the above statements.
- satisfies none of the above statements.
- Los Angeles has about four times as many registered voters as San Diego. A simple random sample of registered voters is taken by each city to estimate the percentage who will vote for school bonds. Assume the percentage who will vote for the school bonds is the same for each city. If a sample of 4,000 voters is taken in Los Angeles and a sample of 1,000 voters is taken in San Diego then the
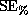 (
(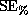 means SE for percent) for the Los Angeles estimate
means SE for percent) for the Los Angeles estimate
- will be about the same as the
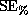 for the San Diego estimate.
for the San Diego estimate.
- will be about twice as big as the
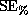 for the San Diego estimate.
for the San Diego estimate.
- will be about four times bigger than the
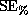 for the San Diego estimate.
for the San Diego estimate.
- will be about half as big as the
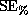 for the San Diego estimate
for the San Diego estimate
- cannot be determined unless the percentage of the sample is given.
- When performing a test of significance,
- rejection of the null hypothesis means that the alternative hypothesis is accepted.
- the alternative hypothesis says that an observed difference is real, not just due to chance error.
- the null hypothesis says that an observed difference is due just to chance error.
- both (b) and (c) are true.
- all of the above statements are true.
- When performing a test of significance, a test statistic
- plays no role in testing hypotheses.
- always follows a normal distribution.
- is used to measure the difference between the data and what is expected under the null hypothesis.
- satisfies both (b) and (c) above.
- satisfies none of the above statements.
- When performing a test of significance,
- the P-value of a test gives the chance that the null hypothesis is true.
- the P-value of a test gives the chance, under the null hypothesis, of getting a test statistic as extreme or more extreme as the observed one.
- the P-value is always computed assuming the null hypothesis is true.
- both (b) and (c) are true.
- all of the above statements are true.
- A newspaper editor of a large town claims that 85% of the people age 18 or over in the town read newspapers and 15% do not. To test his claim a simple random sample of 20 people (aged 18 or over) is taken. Which of the following tests of significance should be used?
- A two sample z-test for the difference in percentages.
- A
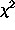 -test (chi-squared test) with 19 degrees of freedom.
-test (chi-squared test) with 19 degrees of freedom.
- A t-test using Student's curve with one degree of freedom.
- A z-test using the normal curve.
- None of the above tests should be used.
- A laser altimeter can measure elevation to within a few inches. As part of an experiment, 25 measurements were made on a mountain peak. These averaged out to be 81,411 inches, and their SD was 30 inches. Which of the following statements is true?
- The elevation of the mountain peak is estimated as 81,411 inches and is likely to be off by 30 inches or so.
- 81,411
 12 inches is a 95% confidence interval for the average of the 25 readings.
12 inches is a 95% confidence interval for the average of the 25 readings.
- 81,411
 12 inches is a 95% confidence interval for the elevation of the mountain peak.
12 inches is a 95% confidence interval for the elevation of the mountain peak.
- About 95% of the readings were in the range 81,411
 12 inches.
12 inches.
- There is a 95% chance that the next reading will be in the range 81,411
 12 inches.
12 inches.
- The two sample z-statistic is calculated using
- the size of the two samples.
- the average of the two samples.
- the SDs of the two samples.
- all of the above.
- none of the above.
- In a certain town there are one million eligible voters. To study the relationship between sex and participation in the last election a simple random sample of size 10,000 was chosen. The null hypothesis is that sex and voting are independent. A test statistic of 3.90 was obtained. Which of the following statements is true?
- The correct P-value is between 10% and 30% based on the
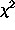 table.
table.
- The correct P-value is between 1% and 5% based on the
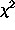 table.
table.
- The correct P-value is between 5% and 10% based on the Student's t table.
- The null hypothesis should be rejected.
- Both (b) and (d) are true.



Eugene Klimko
Thur Nov 18:19:05 EDT 1999
| Top | Home | AnswerKey |
![]()
![]()
![]()