Thomas Zaslavsky's Home Page
at the Department of Mathematics and Statistics of
Binghamton University (SUNY)

Courses

Math 386 (Fall 2024): Combinatorics

Our class home page.
Textbook: Peter Cameron, Combinatorics: Topics, Techniques, Algorithms.

Old Courses

My Math

My Pub(lications) and so forth.
The Home Page of Signed, Gain, and Biased Graphs
with the latest update of my annotated bibliography.
Bonus: A handy guide to German Fraktur letters.

And

My Mother's Math

Publications: Ethnomathematical, cultural, and educational.
Biography
Wikipedia page

The Remainder of This Page

was destroyed and cannot be reconstructed completely. But here is something important:

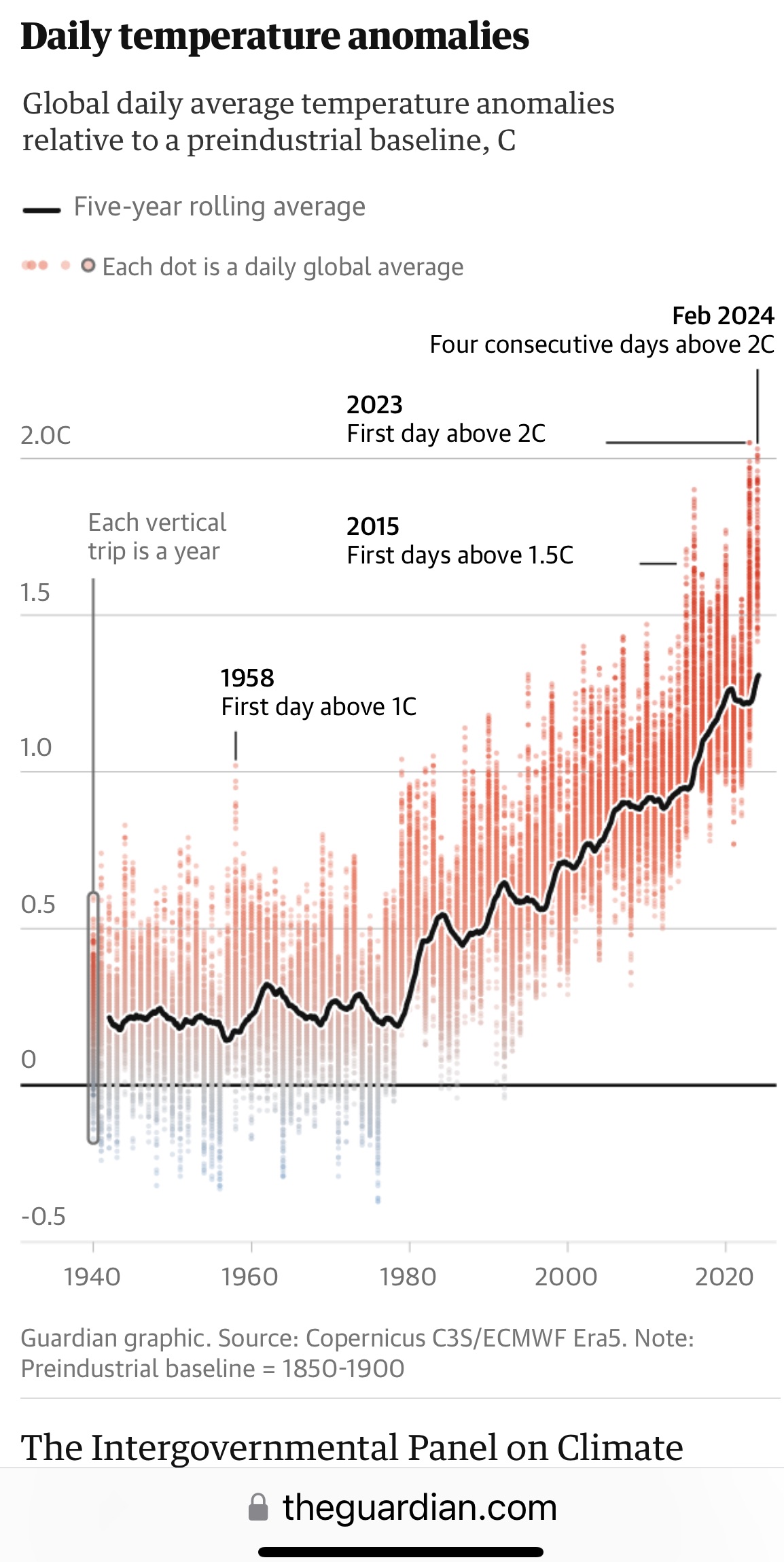
Global warming simplified

This chart from The Guardian, May 8, 2024, shows a fairly steady 0.5C hightened global temperature during 1940-1980 compared to the "pre-industrial" baseline, then a sharp change to a solid rate of condinuing increase.

Guardian chart

The United States of America

"Give me your tired, your poor,
Your huddled masses yearning to breathe free,
The wretched refuse of your teeming shore.
Send these, the homeless, tempest-tost to me,
I lift my lamp beside the golden door!"

—Emma Lazarus, "The New Colussus"

Thomas Zaslavsky's Home Page at the Department of Mathematics and Statistics of Binghamton University (SUNY)