Math 381: Graph Theory Homework Assignments

Go to announcements | course information.

General Advice on Homework

Besides finding the anwer, always try to explain, as well as you can, how you know you have the correct answer.
When solving problems, a systematic solution is better than guesswork. You often may find a solution by intelligent guessing, but then you should look for a way of showing that your solution is correct. This part needs to be systematic if it is to be completely convincing. (This will be clearer after a few days of class!)
Allow 15 minutes per problem (minimum) before you give up, even if you feel you're getting nowhere. These problems need time for thought. If you're still stuck, go on to another problem. Return to the sticky problem later (say, the next day). Often, it then looks easier because you tried hard the first time and then gave your mind time to grind it up-I mean, to come up with ideas. To get the advantage of this method, you have to start the problems well ahead of time. Last-minute effort will not work well in this class.
It's fine to work with other people, indeed I encourage it. However, you should write up your solutions yourself. Here's what you should do:
1. Look at the problem first and think about it for at least a few minutes (preferably more--much more!).
2. Discuss it with other people.
3. Write up a solution in your own words. Don't copy from the notes of your discussion.
I will not accept duplicated work. Anyway, it doesn't do you much good to copy or duplicate someone else's work. The purpose of graded homework is to tell you how well you're doing and how you can improve. That won't happen unless you follow these rules.
If you have any question about the homework grading, you should see me promptly. Maybe you need me to explain something. Or maybe I made a mistake.

Rules for Hand-In Homework.

Hand in a final draft: neat work that is well organized and not cramped. Use as much space as you need. Please also leave some extra space between problems for my comments.
You may discuss hand-in HW with other people, but you must write it up in your own words.
No little stubbies from tearing a page out of your binder. Remove them neatly, please!
Fasten the pages securely. Staples are best. Paper clips and folding a corner don't hold well; don't use them.

HOMEWORK I

Due Wed. 1/24: Read Sect. 11.1.

Do (for class discussion) Ch. 11, ## 1-3

Due Thurs. 1/25: Read Sects. 1.4 and 1.6.

Do Ch. 1, ## 21, 28

Do Ch. 11, ## 6, 9, 11, 13, 14

Due Fri. 1/26: Do Ch. 11, ## 5, 8, 10

Hand in: Ch. 11, ## 4, 7, 12, 16

HOMEWORK II

Due Mon. 1/29: Read Sect. 11.2.

Do Ch. 11, ## 18, 20, 22-24

Due Wed. 1/31:

Do Ch. 11, ## 15, 17, 26, 29, 30

Due Fri. 2/2:

Do Ch. 11, # 33

Due Mon. 2/5: Read Sect. 11.3.

Hand in: Ch. 11, ## 27, 30, 31, 35

HOMEWORK III

Due Wed. 2/7:

Do Ch. 11, ## 11.15, 11.16), 38, A1(a,b)

Due Thurs. 2/8:

Do Ch. 11, # 33 (for Fig. 11.17), 34 (for order <= 5), 39, 43

Due Mon. 2/12: Read Sect. 11.4.

Hand in: Ch. 11, ## 12 (again), 32, 40, A1(c,d)

Problem Set A

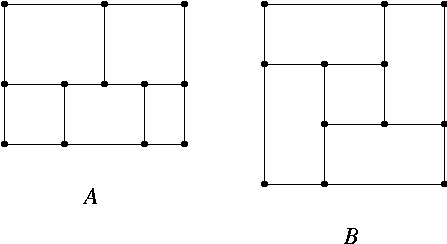
A1. In each graph, find a Hamilton cycle or prove there is none.

(a) Figure 11.18.

(b) Figure 11.16.

(d) Figure 11.40 (right).

HOMEWORK IV

Due Wed. 2/14:

Do Ch. 11, ## 44, 45, 48

Due Thurs. 2/15:

Do Ch. 11, ## 47, 49(a,b), B1(a,b)

Hand in Mon. 2/19:

Ch. 11, ## 49(d), 50, B1(c), B2(c), B3

Due Mon. 2/19:

Read Sect. 11.5.

Do ## B2(a,b), B4

Problem Set B

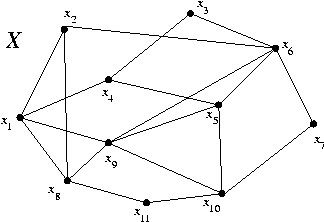
B1. In each graph, find a Hamilton cycle or prove there is none.

(a) Graph X.

(b) Graph Y.

B2. In each graph, find a Hamilton chain or prove there is none.

(a) Graph X.

(b) Graph Y.

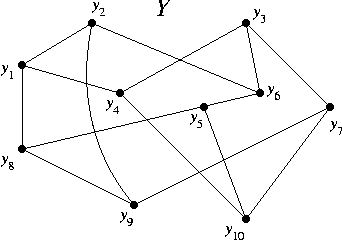
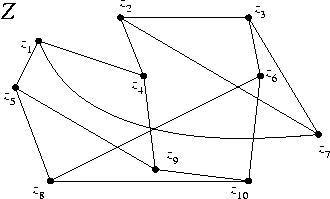
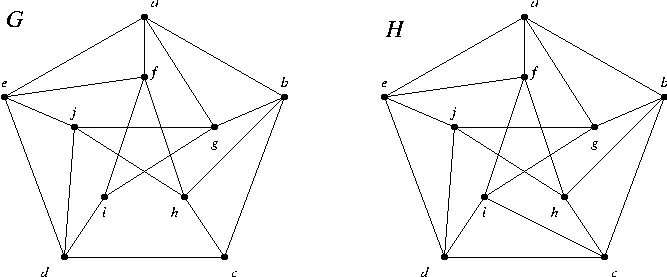
B3. Are the graphs Y and Z isomorphic?

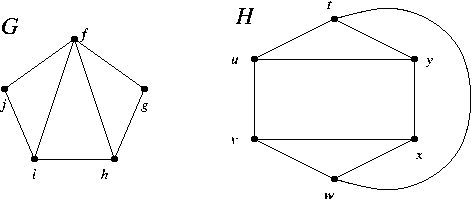
B4. Find a shortest postman tour in graph X.

HOMEWORK V

Due Mon. 2/26:

Read Sect. 11.5.

Due Wed. 2/28:

Do Ch. 11, ## 53, 55-58, 61, 63

Due Thurs. 3/1:

Do Ch. 11, ## 52, 59, 60, 66

Hand in Mon. 3/4:

Ch. 11, ## 54, 62, 64

HOMEWORK VI

Due Mon. 3/5:

Read Sect. 11.7 to the end of page 458.

Due Wed. 3/7:

Do Ch. 11, ## 65, 75-76(a), C1

Due Thurs. 3/8:

Do Ch. 11, ## 69, 70, 75-76(b,c), 77, C2(a)

Due Fri. 3/9:

Do Ch. 11, ## 75-76(e) for (m,n)=(5,4) and (m,n)=(1,n), 79, C2(b)

Hand in Mon. 3/19:

Ch. 11, ## 75-76(d), 75-76(e) for (m,n)=(2,n), C3

Problem Set C

C1. For each number sequence, is it the degree sequence of a tree? If it is, produce a tree whose degree sequence is the given number sequence. You may use Exercise 11.57 as necessary.

(a) (3,3,2,2,1,1,1,1)

(b) (3,3,2,2,2,2,1,1)

C2. In the following diagrams, you need to follow a path from region to region (NOT from vertex to vertex), that starts in any region, goes from one region to another by crossing an edge, crosses every edge exactly once, and doesn't go through any vertex. Can you do it? If not, what is the largest number of edges it is possible to cross?

(a) Diagram A.

(b) Diagram B.

C3. Use Dijkstra's algorithm to find a distance tree in Figure 11.43 with root x, where x is the middle vertex at the bottom. How does it compare with the distance tree rooted at u?

HOMEWORK VII

Due Mon. 3/19:

Read the rest of Sect. 11.7 and all of Sect. 11.6.

Due Wed. 3/21:

Do Ch. 11, ## 80-85(b)

Due Thurs. 3/22:

Do Ch. 11, ## 68 (first and second graphs), D1, D2

Due Fri. 3/23:

Do Ch. 11, # D4

Hand in Mon. 3/26:

Ch. 11, ## 68 (third graph), 86, D3

Problem Set D

D1. Find a minimum-weight spanning tree in Figure 11.38 by Prim's algorithm, starting with vertex d. How does your tree compare with the one found in the book starting from a?

D2. Find a distance tree by Dijkstra's algorithm in Figure 11.38:

(a) Starting with vertex d.

(b) Starting with vertex g.

D3. In Figure 11.38, change all weights 1 to 6. Now:

(a) Find a minimum-weight spanning tree by the greedy algorithm.

(b) Find a minimum-weight spanning tree by Prim's algorithm with starting vertex a. How does it compare with the result from part (a)?

D4. Based on your answers to Problems 80-85(b), what do you expect the answers to be to 80-85(c)? How about the same questions for general K_n? You should try to solve this without actually doing any algorithms. If you come up with answers, can you prove any of them?

HOMEWORK VIII

Due Mon. 4/2:

Read Sect. 12.1, except Example (A Trading Problem) on pp. 482-4 and 485-7, but

do read Lemma 12.1.7 and proof on pp. 484-5.

Due Wed. 4/4:

Do Ch. 12, ## 1, 4, 11 (Fig. 11.15).

Due Thurs. 4/5:

Do Ch. 12, ## 5, 7, 8, 11 (Fig. 11.18).

Hand in Fri. 4/6:

Ch. 12, ## 11 (Fig. 11.19: both graphs), 12, E1.

Problem Set E

E1. Prove that a tournament is transitive if and only if it has no directed cycles.

HOMEWORK IX (with SUPPLEMENT}

Due Wed. 4/11:

Read Ch. 13, pp. 501-505 and to 508 (top).

Do Ch. 13, # 5 (graph 2).

Due Thurs. 4/12:

Do Ch. 13, ## 2, 4, 5 (graph 3) and F1(a-c).

Hand in Wed. 4/18:

Ch. 13, ## 1, 5 (graph 1) and F1(d), F2.

Problem Set F

F1. Find chi(W_k), alpha(W_k), and omega(W_k) (see Announcements for definitions) for

(a) k = 4;

(b) k = 5;

(d) general k.

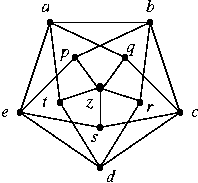
F2. Find chi(G), alpha(G), and omega(G) for the Grötzsch graph shown here:

HOMEWORK X

Due Wed. 4/18: Read all of Sect. 13.1.

Due Thurs. 4/19:

Do Ch. 13, ## 3, 7(a), 9, 10, 15.

Due Fri. 4/20:

Do Ch. 13, ## 7(b,c), 8, 11, G1(a).

Hand in Mon. 4/23:

Ch. 13, ## 6, 12, 16, G1(b).

Problem Set G

G1. Find the chromatic number of graph (a) G, (b) H.

HOMEWORK XI

Due Mon. 4/23:

Read Sects. 13.2-3.

Due Thurs. 4/26:

Do Ch. 13, ## 17, 18, 23, 24, H1(b).

Due Fri. 4/27:

Do Ch. 13, ## 19, 25, 26(a,b), 27, H2(b).

Hand in Mon. 4/30:

Ch. 13, ## 26(c), H1(a), H2(a).

Problem Set H

H1. Find the chromatic polynomial of the graph by the method of deletion and contraction and also, separately, by another method. Check your work by comparing the answers. (a) G. (b) H.

H2. Find the chromatic number of the graph by any method. (a) G. (b) H.

Go to announcements | course information.