Hand in Mon. 2/4: Sect. 1:
HOMEWORK II
For Mon. 2/4:
Due Thurs. 2/7 (for discussion):
Hand in Mon. 2/11: Sect. 2: ## 4, 8(ii), 11, 12.
HOMEWORK III
For Mon. 2/11:
Due Wed.-Thurs. 2/13-14 (for discussion):
Hand in Mon. 2/18:
HOMEWORK IV
For Mon. 2/18:
Due Wed.-Thurs. 2/20-21 (for discussion):
Hand in Mon. 2/25:
HOMEWORK V
For Mon. 2/25:
Due Wed.-Thurs. 2/27-28 (for discussion):
Hand in Mon. 3/4:
Problem Set A
A1. Prove Corollary 6.3.
A2. Prove Corollary 6.4.
A3. Find another method, different from Fleury's, to generate an Eulerian trail.
A4. Find out exactly what's wrong with Exercise 5.8(ii) and, if you can, find a corrected version.
A5. In each graph, find a Hamilton cycle or prove there is none.
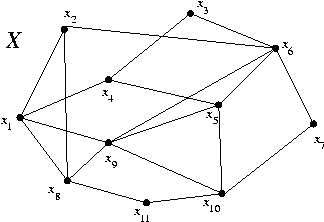
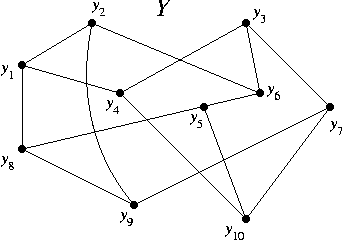
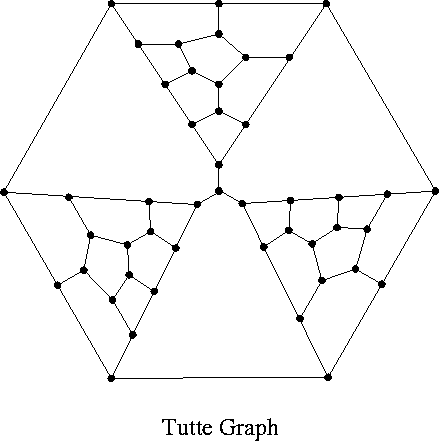
HOMEWORK VI
For Mon. 3/4:
Due Wed. 3/6 (for discussion):
Also, review for Test I.
HOMEWORK VII
For Mon. 3/11:
Due Wed. 3/13 (for discussion):
Due Thurs. 3/14 (for discussion):
Hand in Mon. 3/18:
Problem Set B
- Find all unlabelled trees (that means: isomorphic trees are considered to be the same) on n vertices for n = 1, 2, ..., 5.
- Find a cycle in the Petersen graph by using the method of Lemma 6.1 . This means to go through the details of the proof of the lemma, using the method (not in a clever way) to eventually wind up with a cycle.
- Prove: Proposition. A forest is a simple graph.
HOMEWORK VIII
For Mon. 3/18:
Due Thurs. 3/21:
Due Fri. 3/22:
Hand in Wed. 4/3:
Problem Set C
- Hamiltonicity:
- Show that H has a unique Hamiltonian cycle.
- Find all edges e such that H-e has no Hamiltonian cycle.
- Planarity:
- Decide whether H is planar.
- Let H' be H with the edges x6x7 and x10x12 added. Decide whether H' is planar. Use two different methods if you can find the time.
The problems refer to the graph H shown. (This is the same H as on the last test.)
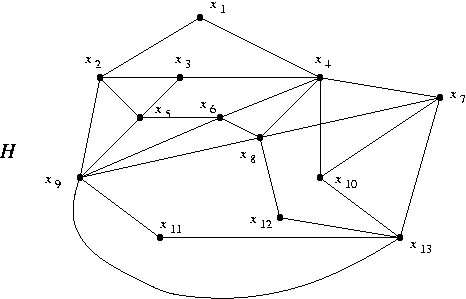
HOMEWORK IX
For Wed. 4/3:
Due Thurs. 4/4:
Due Fri. 4/5:
Hand in Mon. 4/8:
HOMEWORK X
For Mon. 4/8:
Due Thurs. 4/11:
Due Fri. 4/12:
Hand in Mon. 4/15:
HOMEWORK XI
For Wed. 4/17:
Due Thurs. 4/18:
Hand in Mon. 4/22:
Problem Set D
- Use the inductive method of the proofs of Theorems 17.1 and 17.3 to actually color the graph G in 5 colors. (This is the correct problem. The previously announced version with 4 was a mistake. Sorry.)
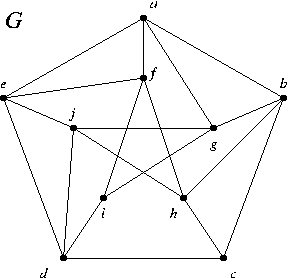
HOMEWORK XII
For Mon. 4/22:
Due Mon. 4/22 (changed to Fri. 4/26):
Due Wed. 4/24 (changed to Fri. 4/26):
HOMEWORK XIII
For Mon. 4/29:
Due Wed. 5/1:
Due Thurs. 5/2:
Hand in Fri. 5/3:
HOMEWORK XIV
For Fri. 5/3:
Due Mon. 5/6:
Due Wed. 5/8:
Hand in Wed. 5/8:
HOMEWORK XV
Due Thurs. 5/9:
Problem Set E
- Deduce the vertex Menger's theorem 28.2 from the edge Menger's theorem 28.1. (NOTE: This problem seems to be a mistake.)
- Deduce the undirected edge Menger's theorem 28.1 from the directed edge Menger's theorem 28.5.
- Theorem 28.5 is a digraph version of Theorem 28.1. Theorem 28.7 (see the statement and the associated definitions), which the author forgot to print, is a digraph version of Theorem 28.2.
- Deduce Theorem 28.7 from Theorem 28.5.
- Deduce Theorem 28.2 from Theorem 28.7.
- Verify Theorem 28.7 for each digraph in Figure 28.7.
- Find the chromatic number of the following graph.
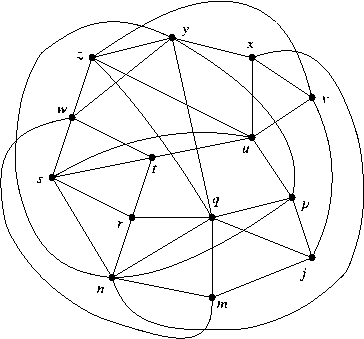
- Let G be a simple graph of order n >= 3 having m edges.
- Prove that cr(G) >= m - 3(n-2).
- If G has no triangles, then cr(G) >= m - 2(n-2).
- Let H = Kr,r - M where M is the edge set { xiyi : i = 1, 2, ..., r }.
- Find out as much as you can about the thickness t(H).
- Also find out as much as you can about cr(H).
- In the graph of Problem E4, verify Menger's Theorems 28.1 and 28.2 between the vertices s and p. This means: find the number k which is both the largest number of edge-disjoint (or, internally disjoint) sp-paths and the smallest number of edges whose removal disconnects s from p.
For additional practice, try other pairs of vertices. Each different pair is a different problem. - Let G be a simple graph of order n >= 3 having m edges.
Go to announcements | course information | syllabus.