Math 381: Graph Theory Homework Assignments

A2. Suppose G is a simple graph of order n, V = {v₁,v₂,...,v_n} is its vertex set, and A is its adjacency matrix. Show that, for any length m>0, the number of walks of length m from v_i to v_j equals the (i,j) entry of A^m.

A3. (Advanced problem, for those who are interested.) Let G be any graph. Define a relation on its vertex set V by v ~ w if there is a path from v to w.

Prove that ~ is an equivalence relation.
Prove that v ~ w if and only if v and w are in the same component of G (using the book's definition of component).
Prove that G is connected if and only if ~ has just one equivalence class.

HOMEWORK IV (2/7)

For Mon. 2/10:

Read Sect. 7.
For Thurs. 2/13 (for discussion):

Do Sect. 7: ## 1-5.

Do ## B1, B3, B5.
For Fri. 2/14 (for discussion):

Do Sect. 7: ## 6-8.

Do ## B4, B6(a).
Hand in Mon. 2/17:

7.9, B2, B6(b,c).

Don't overlook the corrections!

Problem Set B

B1. Prove Corollary 6.3.

B2. Prove Corollary 6.4.

B3. Find another method, different from Fleury's, to generate an Eulerian trail.

B4. Find out exactly what's wrong with Exercise 5.8(ii) and, if you can, find a corrected version.

B5. Define S_n = {1,2,3,...,n}.
Now, G is the graph defined as follows: the vertex set consists of all 3-element subsets of S₁₀ , that is,

V(G) = {X subset of S₁₀ : |X| = 3 }
and two vertices X and Y are adjacent if and only if they are disjoint, that is, (X intersect Y) = null set. Is G connected?

B6. In each graph, find a Hamilton cycle or prove there is none.

(a) Graph X.

(b) Graph Y.

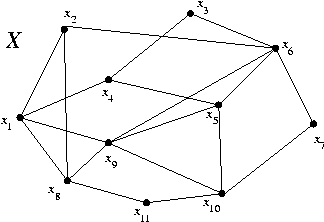
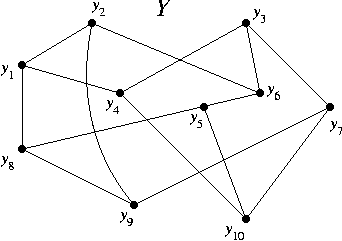
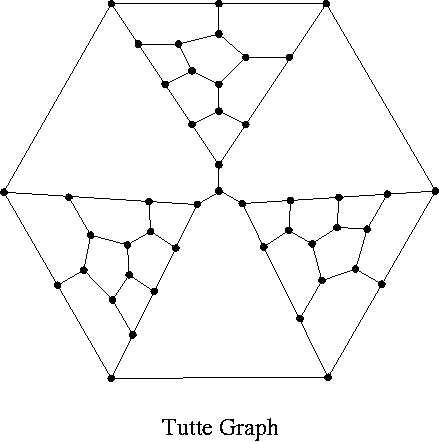
HOMEWORK V (2/7)

For Mon. 2/17:

Read Sect. 8 to page 40.
For Wed. 2/19 (for discussion):

Do Sect. 8: # 1 for (A,G), (B,C), and (D,E); # 4.

Also, Sect. 7 # 10 is nice if you want to have fun with graphs.
Also, review for Test I.

HOMEWORK VI (2/21)

For Mon. 2/24:

Read Sect. 9 and the following parts of Sect. 11:

"The minimum connector problem" (to the proof of Theorem 11.1, inclusive) and "Enumeration of chemical molecules".
For Thurs. 2/27 (for discussion):

Do ## C1, C2;

Sect. 9: ## 3, 4, 6, 7(i-iv).
For Fri. 2/28 (for discussion):

Do # C3;

Sect. 9: ## 8(i), 10(i);

Sect. 11: ## 1, 3, 4(i), 7.
Hand in Mon. 3/3:

Sect. 9: ## 2, 5, 7(v), 8(ii), 9; and # 11.2.

Problem Set C

Find all unlabelled trees (that means: isomorphic trees are considered to be the same) on n vertices for n = 1, 2, ..., 5.
Find a cycle in the Petersen graph by using the method of Lemma 6.1 . This means to go through the details of the proof of the lemma, using the method (not in a clever way) to eventually wind up with a cycle.
Prove: Proposition. A forest is a simple graph.

HOMEWORK VII (2/21)

For Mon. 3/3:

Read Sects. 10 and 12, and (optional; interesting for computer science) Sect. 11 ``Searching trees''. (See corrections for Sect. 10.)
For Thurs. 3/6:

Do Sect. 10 ## 2(i) (and also go back from the tree to the sequence, as a check), 2(ii) (and also go back from the sequence to the tree, as a check), 3, 4;

Sect. 12 ## 2-4, 6, 7.
For Fri. 3/7:

Do # D1;

Sect. 10 # 6;

Sect. 12 ## 5(i), 8, 10(K_4,3).
Hand in Mon. 3/17:

Sect. 10: ## 2(ii)(second graph) (and also go back from the sequence to the tree, as a check), 5;

Sect. 12 ## 5(ii), 9, 10(Petersen graph);

# D2.

Problem Set D

The problems refer to the graph H shown.

Hamiltonicity:
1. Show that H has a unique Hamiltonian cycle.
2. Find all edges e such that H-e has no Hamiltonian cycle.
Planarity:
1. Decide whether H is planar.
2. Let H' be H with the edges x₆x₇ and x₁₀x₁₂ added. Decide whether H' is planar. Use two different methods if you can find the time.

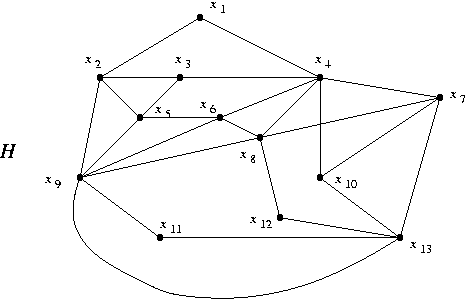
HOMEWORK VIII (3/6)

For Mon. 3/17:

Read Sects. 13 and 14.
For Thurs. 3/20:

Do Sect. 13 ## 1(i-iii), 2(i), 3(i), 4.
For Fri. 3/21:

Do Sect. 13 ## 2(ii), 3(ii), 6, 8(i), 9.

Do Sect. 14 # 1 (see the correction).
Hand in Mon. 3/24:

Sect. 9: # 2 for 6 vertices only, with proof.

Sect. 13: ## 1(iv), 5, 7, 8(ii), 10 (see the correction).

Sect. 14: # 2.

HOMEWORK IX (3/28)

For Mon. 3/31:

Read Sects. 15 and 17.
For Thurs. 4/3:

Do Sect. 15 ## 1-5, 6(i), 7.

Do Sect. 17 ## 1, 4, 7.
For Fri. 4/4:

Do Sect. 15 ## 6(ii), 9.

Do Sect. 17 ## 2, 3, 6, 8, 10, 11(i).
Hand in Mon. 4/7:

Sect. 15: ## 10.

Sect. 17: ## 5, 9 (see correction), 11(ii,iii).

HOMEWORK X (3/28)

For Mon. 4/7:

Read Sects. 18, 19 and 20.
For Thurs. 4/10:

Do Sect. 19 ## 1(i), 2(cube, iscosahedron), 3, 5, 7.

Do Sect. 20 ## 1, 3(graphs 17-18).
For Fri. 4/11:

Do Sect. 20 ## 3(graphs 19-21), 4, 6, 8, 9; and # E1. (The ``D1'' in the handout was an error.)
Hand in Mon. 4/14:

Sect. 19: ## 1(ii), 4.

Sect. 20: ## 2, 7, 10.

Problem Set E

Use the inductive method of the proofs of Theorems 17.1 and 17.3 to actually color the graph G in 5 colors.

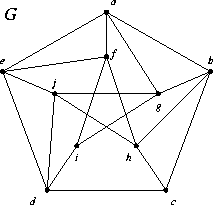
HOMEWORK XI (4/11)

For Mon. 4/14:

Read Sect. 21.
For Wed. 4/18:

Do Sect. 21 ## 1, 2 (do any two of the six graphs), 3, 5, 6.

HOMEWORK XII (4/11)

For Wed. 4/23:

Read Sect. 22 (to the proof of Theorem 22.1; omit the critical path problem) and Sect. 25.
For Fri. 4/25:

Do Sect. 22 ## 1, 2, 5.

Do Sect. 25 ## 1, 3, 5. (See correction.)
For Mon. 4/28:

Do Sect. 25 # 6(i).

Do ## F1, F2.
Hand in Mon. 4/28:

Sect. 21, ## 4, 7.

Sect. 25 ## 2, 4, 6(ii).

# F3.

Problem Set F

Find the chromatic number of the ``clock'' graph G defined by
V(G) = {1,2,...,12},

E(G) = { {i,i+1}, {i,i+3}, {i,i+6} : i = 1,2,...,12 },
where in computing i+1, etc., arithmetic is modulo 12; that is, we treat 13 as if it were 1, 14 as if it were 2, etc.
Prove: if every vertex of a graph has even degree, then every cutset has an even number of edges.
Suppose G is a graph without loops. For a vertex v, define T = the set of all edges incident with v. Prove that there are cutsets D₁, ..., D_k (where k >= 1) such that the cutsets are pairwise disjoint and their union is T.

HOMEWORK XIII (5/2)

For Mon. 5/5:

Read Sect. 28.
For Mon. 5/5:

Do Sect. 28 ## 1, 2(i), 4(i), 5(i), 6.

Do ## G1, G2a(first digraph).
For Wed. 5/7:

Do Sect. 28 ## 4(ii), 5(ii).
Hand in Wed. 5/7:

Sect. 28 ## 2(ii), 4(iii), 5(iii).

## G2b, G2a(second digraph).

HOMEWORK XIV (5/2)

For Thurs. 5/8:

Do ## G2(c), G3-G6.

Problem Set G

Deduce the undirected edge Menger's theorem 28.1 from the directed edge Menger's theorem 28.5.

Theorem 28.5 is a digraph version of Theorem 28.1. Theorem 28.7 (see the statement and the associated definitions), which the author forgot to print, is a digraph version of Theorem 28.2.
1. Verify Theorem 28.7 for each digraph in Figure 28.7.
2. Deduce Theorem 28.2 from Theorem 28.7.
3. Deduce Theorem 28.7 from Theorem 28.5.
Find the chromatic number of the graph F. (Note: This is the corrected graph F that has no K₄ subgraph.)
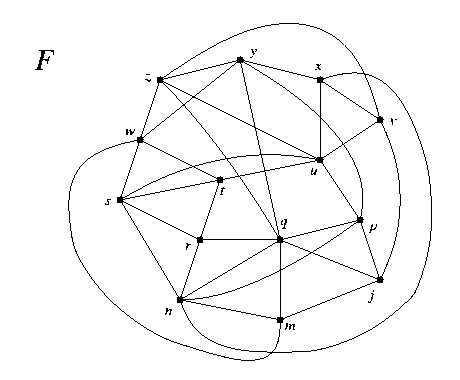
Let G be a simple graph of order n >= 3 having m edges.
1. Prove that cr(G) >= m - 3(n-2).
2. If G has no triangles, then cr(G) >= m - 2(n-2).
Let H = K_r,r - M where M is the edge set { x_iy_i : i = 1, 2, ..., r }. (Notation: The two bipartite vertex sets of K_r,r are V₁ = { x₁, x₂, ..., x_r } and V₂ = { x₁, x₂, ..., x_r } . The edges are x_iy_j for i, j = 1,2,...,r.)
1. Find out as much as you can about the thickness t(H).
2. Also find out as much as you can about cr(H).
I suggest that you start with small values of r.
In the graph F, verify Menger's Theorems 28.1 and 28.2 between the vertices s and p. This means: find the number k which is both the largest number of edge-disjoint (for the vertex theorem, internally disjoint) sp-paths and the smallest number of edges (for the vertex theorem, vertices) whose removal disconnects s from p.
For additional practice, try other pairs of vertices. Each different pair is a different problem, so you can get a lot of practice from this one graph.

General Advice on Homework

Besides finding the anwer, always try to explain, as well as you can, how you know you have the correct answer.
When solving problems, a systematic solution is better than guesswork. You often may find a solution by intelligent guessing, but then you should look for a way of showing that your solution is correct. This part needs to be systematic if it is to be completely convincing. (This will be clearer after a few days of class!)
Allow 15 minutes per problem (minimum) before you give up, even if you feel you're getting nowhere. These problems need time for thought. If you're still stuck, go on to another problem. Return to the sticky problem later (say, the next day). Often, it then looks easier because you tried hard the first time and then gave your mind time to grind it up-I mean, to come up with ideas. To get the advantage of this method, you have to start the problems well ahead of time. Last-minute effort will not work well in this class.
It's fine to work with other people, indeed I encourage it. However, you should write up your solutions yourself. Here's what you should do:
1. Look at the problem first and think about it for at least a few minutes (preferably more--much more!).
2. Discuss it with other people.
3. Write up a solution in your own words. Don't copy from the notes of your discussion.
I will not accept duplicated work. Anyway, it doesn't do you much good to copy or duplicate someone else's work. The purpose of graded homework is to tell you how well you're doing and how you can improve. That won't happen unless you follow these rules.
If you have any question about the homework grading, you should see me promptly. Maybe you need me to explain something. Or maybe I made a mistake.

Rules for Hand-In Homework.

I expect complete written solutions that give full justification of the correctness of your answer. Answers without any justification will not be accepted. You'll gradually learn better what this means, so don't worry now, just do your best to explain your work.
Hand in a final draft: neat work that is well organized and not cramped. Use as much space as you need. Please also leave some extra space between problems for my comments.
You may discuss hand-in HW with other people, but you must write it up in your own words.
No little stubbies from tearing a page out of your binder. Remove them neatly, please!
Fasten the pages securely. Staples are best. Paper clips and folding a corner don't hold well; don't use them.

Go to announcements | course information | syllabus.