These problems are for extra study; they are recommended but not required. They may need more thought than most of the homework problems have. We may discuss them in class during the last days.
N1. Let N5 = {1,2,3,4,5}. Define a graph G5 by V(G5) = the set of all unordered pairs ij of elements of N5, with two pairs ij and kl adjacent if their intersection is empty.
(a) Prove that G5 cong P, where P = Petersen graph.
(b) Prove that, for any two vertices x, y of P, there is an isomorphism phi of P with itself such that phi(x) = y. (Technically, phi is the one-to-one correspondence between vertex sets. You can think of it as the function which tells you which vertex y will be relabelled x in the relabelling process.)
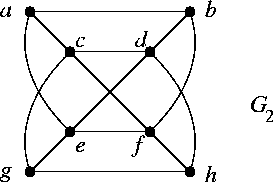
N2. The graph G2 is shown. Find out as much as you can about its crossing number.

N3. (a) Find a largest graph with 11 vertices and all degrees divisible by 3. (b) Even better, find all (nonisomorphic) largest such graphs.
N4. In class we proved that theta(G) <= cr(G)+1. Can you improve on this, e.g., by reducing the upper bound?