Homework Set IIa (1/30)

Do for discussion Thurs. 2/5 (additional problem):
# BB1.

Problem Set BB

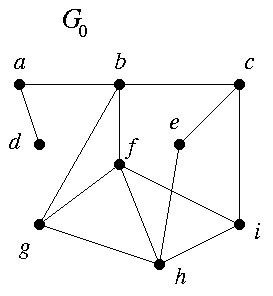
BB1. This concerns Theorem 1.1.2 and the example G₀. I'll follow the book's notation. The sequence
   (S1) (4, 4, 4, 3, 3, 3, 2, 2, 1)
is known to be graphic, because it is the degree sequence of G₀. From (S1) the rule of Theorem 1.1.2 gives
   (S2) (3,3,2,2,3,2,2,1),
which, rearranged in descending order, is
   (S3) (3,3,3,2,2,2,2,1).

1. (a) In this example what are s, t₁, ..., t_s, n, d₁, ..., d_n ? (Give their values.)
2. (b) Label the vertices of G₀ by S, T₁, ..., T_s, D₁, ..., D_n as in the proof of the theorem.) Do this problem for each of the three possible choices of S.
3. (c) If you delete vertex S, does the new graph G₀ - S have (S3) as its degree sequence?
4. (d) Use the method in the proof to modify G₀ so that, when you delete S, you do get (S3) as the degree sequence of the new graph.