For Mon. 2/2: Read Section 1.3.
Do for discussion Thurs. 2/5:
Sect. 1.2, # 9 (graphs 1 and 3 only).
Sect. 1.3, ## 1, 2, 5, 11.
## C2, C5(a).
Do for discussion Fri. 2/6:
Sect. 1.3, ## 12-14, 16.
## C3, C5(b).
Hand in Mon. 2/9:
Sect. 1.2, # 10 and the rest of # 9.
Sect. 1.3, # 7.
## C1, C4, C7.
Notation: Since I can't use full mathematical notation on the Web, I'll write G-, here only, for the complement of G. I'll write "G isom H" to mean G and H are isomorphic.
C1. CORRECTION: Omit this problem.
C2. In the graph F of Figure 1.1.16:
(a) Find a longest path P. (Call its endpoints x and y.)
(b) Pick an edge e of P which lies in a cycle of F. In F - e, find a path connecting x and y.
(c) Pick an edge f of P which does not lie in a cycle of F. In F - f , is there a path connecting x and y?
C3. Let G be a graph which has a cycle. Let C be a cycle in G. Let a, b be arbitrary vertices in G, and let e be any edge in C. Explain why, if G has a path connecting a to b, so does G - e.

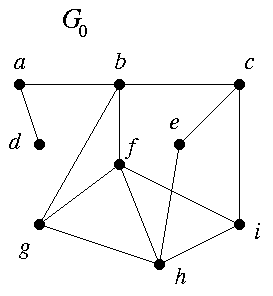
C4. Show that the graph G0 is not a tree by using the proof of the first half of Theorem 1.3.5. Namely, pick any two paths you like between a and e, and use the method in the proof to contruct a cycle in G0.
C5. In G2 from Homework I, find the values of
(a) lambda(1, 5), (b) lambda(2, 6).
Use Menger's Edge Theorem to prove you are correct: i.e., find the pairwise edge-disjoint paths that the theorem tells us exist.
C6. The same as C5, but for lambda(v3, v5) in G3 from Homework I.