Homework Set II (1/23)

For Mon. 1/26: Read Sections 1.1, 1.2.

Do for discussion Thurs. 1/29:
Sect. 1.1, ## 1, 2, 4(a-c), 6, 9(a).
Sect. 1.2, # 1, 5, 7, 8.
# B3(a).

Do for discussion Fri. 1/30:
Sect. 1.2, ## 2, 3.
## B1, B2, B3(b).

Hand in Mon. 2/2:
Sect. 1.1, ## 3, 4(d), 5, 7, 8, 9(b).
Sect. 1.2, ## 4, 6.
# B4.

Problem Set B

Definitions will be found on the announcements page.

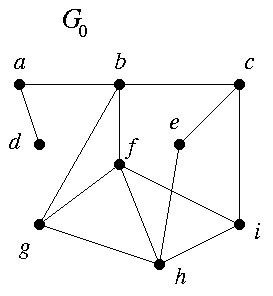
B1. This concerns Theorem 1.1.2 and the example G₀. I'll follow the book's notation. NOTE: There are some errors in this question. The corrected version is Problem # BB1 in HW Set IIa.) The sequence
   (S1) (4, 4, 4, 3, 3, 3, 2, 2, 1)
is known to be graphic, because it is the degree sequence of G₀. From (S1) the rule of Theorem 1.1.2 gives
   (S2) (3,3,2,2,3,2,2,1).

1. (a) In this example what are s, t₁, ..., t_s, n, d₁, ..., d_n ? (Give their values.)
2. (b) Label the vertices of G₀ by S, T₁, ..., T_s, D₁, ..., D_n as in the proof of the theorem. (Note: Do not choose S = h.)
3. (c) If you delete vertex S, does the new graph G₀ - S have (S2) as its degree sequence?
4. (d) Use the method in the proof to modify G₀ so that, when you delete S, you do get (S2) as the degree sequence of the new graph.

B2. In which graphs is the whole vertex set V the only separating set?

B3. In G₂ from Homework I, find the values of (a) kappa(1, 5), (b) kappa(2, 6). Use Menger's Vertex Theorem to prove you are correct: i.e., find the internally disjoint paths that the theorem tells us exist.

B4. The same as B3, but for kappa(v₃, v₅) in G₃ from Homework I.