Homework Set VIIIa and Problem Set HH (3/17)

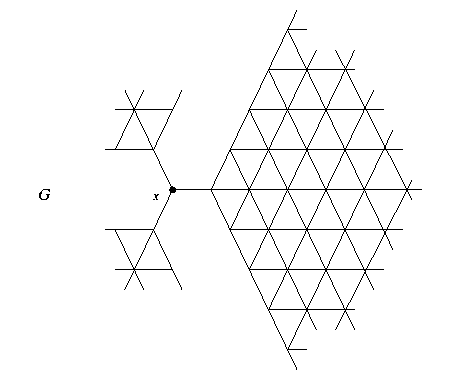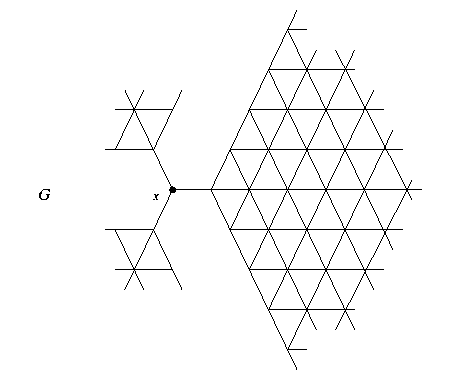
Do for discussion on Mon. 3/22:
## HH1(a), HH2(a).

Do for discussion on Wed. 3/24:
## HH1 and HH2: in each, do one or two of (b,c,d).
# HH3.

Problem Set HH

HH1. Use the proof method of Theorem 3.2.4 to decompose into subgraphs isomorphic to P₃ :

1. the Petersen graph, Fig. 1.1.13,
2. the icosahedral graph I in Fig. 1.2.5,
3. Fig. 2.3.4,
4. the Tutte graph, Fig. 2.3.5.

HH2. Use the proof method of Theorem 3.1.7 (Listing's Theorem) to decompose into the smallest possible number of trails:

1. the Petersen graph, Fig. 1.1.13,
2. Fig. 2.3.6,
3. Fig. 2.3.7,
4. the Grötzsch graph, Fig. 2.1.6.

HH3. Do your best to give a correct proof that, in the infinite graph G shown here, each of the three lobes hanging off vertex x has a 1-way Eulerian trail. (All the lobes are the same, but I only drew a large part of one of them.)