Homework Set IX and Problem Set I (3/26)

For Mon. 3/29:
Read Sects. 4.1 and 4.2.

Do for discussion Thurs. 4/1:
Sect. 4.1, ## 1, 2, 4, 6.
Sect. 4.2, ## 2(a), 3.
# I1(a).

Do for discussion Fri. 4/2:
Sect. 4.1, ## 7, 8.
Sect. 4.2, ## 2(b), 4, 6.
# I2(a).

Hand in Wed. 4/14:
Sect. 4.1, ## 3, 5.
Sect. 4.2, ## 1, 2(c).
## I1(b), I2(b).

Problem Set I

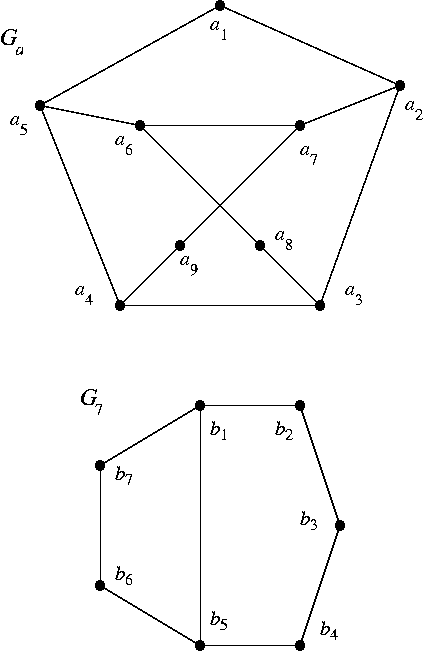
I1. This question concerns the proof of Theorem 4.1.2* (that is, the base case k = 2 of Turan's Theorem). You are given the ``starting'' graph G of the proof, which has no triangle.
(i) Construct the new graph H in the proof of Theorem 4.1.2*. What are your x and W?
(ii) Compare the degrees of the vertices in G and H.
(iii) Compare q_G and q_H. Which is larger? Why is that significant for the proof of the theorem?
(iv) Compare H to the largest possible triangle-free graph on the same number of vertices. How are they similar?

(a) For G = G_a, the Petersen graph with one vertex deleted. (See below.)
(b) For G = G₇, shown below.

I2. The uniqueness of the maximum graph in Theorems 4.1.2* and 4.1.2 is not proved in the book.
(a) Prove uniqueness in Theorem 4.1.2*.
(b) Prove uniqueness in Theorem 4.1.2.