Good Advice and General Instructions on Homework Problems and Solutions
This assignment is for discussion in class (except "Hand In"). Come up with IDEAS and bring them all along!

Due Wed., 1/30:
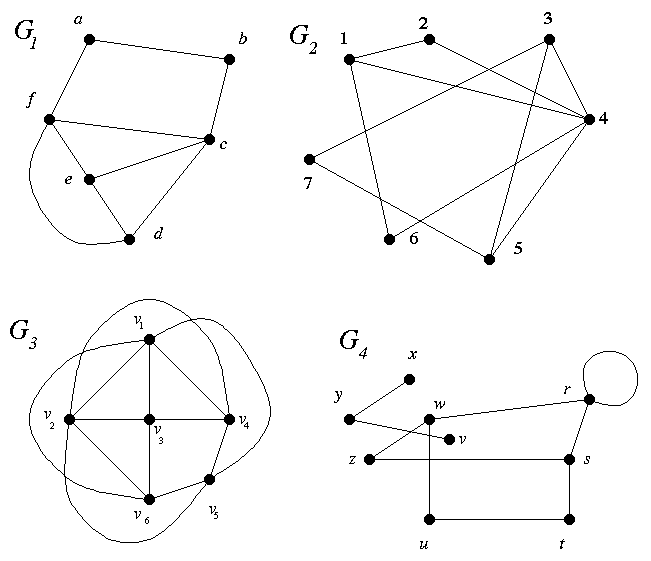
Do ## A1, A2, A4 for G = G1 (do this first) and G2, G4.
Also, read Section 1.1.
Also, read the course information page and the homework instructions.
Due Fri. 2/1:
# A3 (again, do G1 first).
Hand in Wed. 1/30:
## A1–A4 for G3.
Some terminology about a graph (from the announcements page):
A1. (a) Find a separating set. (b) Find one that is smallest.
A2. (a) Find a disconnecting set. (b) Find one that is smallest.
A3. Write down the degree sequence of G = G1, G2, G3. (Omit G4.)
A4. Treat G as a graph in which the vertices stand for people and the edges join pairs who don't get along together, so they can't be on the same committee. What is the largest possible committee?
Due Fri., 2/1:
Hand in Mon., 2/4:
Due Mon., 2/4:
B1. This problem concerns ways of testing graphs for being isomorphic or nonisomorphic. In each part, suppose G and H are isomorphic graphs.
The point is that, if G and H are graphs that fail any one of these properties, then they cannot be isomorphic (by contradiction). But the converse is not true, as the next problem shows.
B2. For each property in # 1, find a pair of graphs, G and H, that are not isomorphic but which have the property. Specifically:
Homework Set II (1/28)
Read Section 1.2.
## B1(a,b), B2(a,b).
Do for discussion:
## B1(c), B2(c) (think about them for a few minutes; we'll discuss them in class).
Problem Set B
Go to homework index.
For Tues. 2/5: Read Section 1.3.
Do for discussion Tues. 2/5:
Do for discussion Wed. 2/6:
Hand in Fri. 2/8:
C1. This concerns Theorem 1.1.2 and the example G0. I follow the book's notation.
The sequence
C2. In the graph F of Figure 1.1.16:
C3. Let G be a graph which has a cycle. Let C be a cycle in G. Let a, b be arbitrary vertices in G, and let e be any edge in C. Explain in detail why, if G has a path connecting a to b, so does G − e.
Homework Set III (2/4)
Remember to check the announcements page for corrections to the textbook.
Sect. 1.1, ## 1, 2, 4(a-c), 6.
Sect. 1.2, # 1, 4, 7.
Sect. 1.1, # 9.
Sect. 1.2, ## 2, 3, 6, 8.
# C2.
Sect. 1.1, ## 3, 4(d), 5, 7, 8.
Sect. 1.2, # 5.
## C1, C3.
Problem Set C
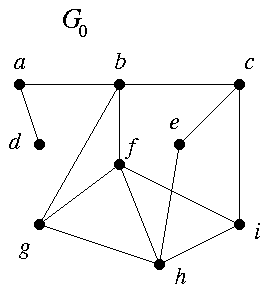
(S1) (4, 4, 4, 3, 3, 3, 2, 2, 1)
is known to be graphic, because it is the degree sequence of G0. From (S1) the rule of Theorem 1.1.2 gives
(S2) (3,3,2,2,3,2,2,1),
which, when rearranged in descending order, is
(S3) (3,3,3,2,2,2,2,1).
Go to homework index.
For Fri. 2/8: Read Section 2.1.
Do for discussion Tues. 2/12:
Do for discussion Wed. 2/13:
Hand in Fri. 2/15:
Homework Set IV (2/4)
Sect. 2.1, ## 1-4, 8, 13, 18, and 9-10 (for P5, K4,4, D, and O).
## D1, D3.
Sect. 2.1, ## 6, 11, 14, 16, 17.
# D4.
Sect. 2.1, ## 5, 7, 15(a), 19, 20 (see announcement), and 9-10 (for I).
## D2, D5.
Textbook Corrections
Always remember to check the announcements page for corrections!
D1. Suppose G is a connected graph whose average degree is > 2.
(a) Prove that G contains at least 2 cycles.
(b) Prove that it is possible for G to have exactly 2 cycles.
D2. Suppose G is a connected graph whose average degree is 3.
(a) Show that G has at least 4 cycles.
(b) Is 4 the best possible number? Or can you prove that G must have 5 or more cycles? 6 or more?
D3. Find the chromatic number χ(G) where G is the graph in Figure 2.1.5.
D4. Is the graph of Figure 2.1.5 critical? Prove. (Don't believe everything you read!)
D5. Is the graph of Figure 2.1.6 critical? Prove.
For Mon. 2/18: Read Sections 2.2, 2.3.
Do for discussion Tues. 2/19:
Do for discussion Wed. 2/20:
Hand in Fri. 2/22:
Homework Set V (2/16)
Sect. 2.2, ## 3, 5, 6.
Sect. 2.3, ## 1-3.
## E1(a), E5(a), E7(a,b).
Sect. 2.2, ## 8, 9.
Sect. 2.3, ## 4, 5-7 (for Q3 and I), 8, 10, 12.
## E5(b,c), E7(c).
Sect. 2.2, ## 4, 7, 10.
Sect. 2.3, ## 5-7 (for D), 17.
## E1(b), E2, E5(d), E6, E7(d).
Textbook Corrections
E1. Prove there is no 1-factor in the graph of Figure 2.2.6 (a) left, (b) right.
E2. Is the graph of Figure 2.1.2 critical? Prove.
The first example graph theorists look at when they have a complicated new idea is Kp. The next one could be Kp − edge.
E3. Let G = Kp − edge. Find the chromatic number χ(G).
E4. Let G = Kp − edge. Find the edge chromatic number χ'(G) when p is even, i.e., p = 2n (n ≥ 1).
E5. Let V(K2n) = {0, 1, 2, ..., 2n−2, x}. We have a standard way to decompose K2n into 1-factors (see Section 2.2). In K8, which "standard" 1-factor contains the following edge? (For your answer you may list all edges that belong to the 1-factor.)
(a) 23.
(b) 2x.
(c) 36.
(d) 15.
E6. Prove that, if G is a tree, then its edge chromatic number χ'(G) equals its maximum degree Δ(G).
E7. Find a Hamilton cycle or prove there is none.
(a) Figure 2.3.4.
(b) Figure 2.3.5. (Hint: there isn't!)
(c) Figure 2.1.6.
(d) Figure 2.3.7.
Do for discussion Tues. 2/26:
Do for discussion Wed. 2/27:
Hand in Fri. 3/1:
Homework Set VI (2/24)
Read Sections 2.4, 3.1. (The proofs in 3.1 show you how to construct trails, decompositions, etc.)
Sect. 2.3, ## 7 (for graph I), 18(a).
Sect. 2.4, ## 1, 4, 5.
Sect. 3.1, ## 1-3, 4 (for Q3, K4,4 only), 7.
Sect. 2.3, ## 18(b).
Sect. 2.4, ## 2, 8.
Sect. 3.1, ## 5, 8, 11.
## F1(a,b).
Sect. 2.3, # 18(c).
Sect. 2.4, ## 7, 25.
Sect. 3.1, ## 6, 12.
## F1(d).
Textbook Corrections
F1. Let V(K2n+1) = {0, 1, 2, ..., 2n-1, x}. We have a standard way of decomposing K2n+1 into Hamilton cycles (see Section 2.3). In K11, which "standard" Hamilton cycle contains the edge
(a) 23 ?
(b) 3x ?
(c) 46 ?
(d) 37 ?
TEST I will be on Tuesday, Mar. 12 (changed from Mar. 5).
Read Section 3.2.
Do for discussion Tues. 3/5:
Do for discussion Wed. 3/6:
Hand in Fri. 3/8:
G1. Decompose into the fewest possible trails:
G2. Decompose into the fewest possible paths: (a, b, c) from #G1.
G3. Decide whether the graph is Hamiltonian (i.e., has a Hamilton cycle):
G4. Verify that, in the proof of Theorem 2.3.2, the first two 1-factors unite to form a Hamilton cycle. Your proof should be valid for all n ≥ 2.
G5. Let G = Kp − edge. Find the edge chromatic number χ'(G) when p is odd, i.e., p = 2n−1 (with n ≥ 2).
G6. (a) Find a graph E which has an Eulerian circuit but no Hamilton cycle.
G7. Produce a decomposition of Fig. 3.2.8 into two 2-factors, using the method of proof of Theorem 3.1.4.
G8. Prove that Kp can be decomposed into p − 1 paths P1, P2, ..., Pp−1 for all values of p, not only the even values to which Theorem 2.3.4 applies.
G9. Use the proof method of Theorem 3.2.4 to decompose into subgraphs isomorphic to P3 :
G10. Use the proof method of Theorem 3.1.7 (Listing's Theorem) to decompose into the smallest possible number of trails:
G11. (Optional: research problem.) We know some cubic graphs can be decomposed into P3 subgraphs (e.g., Figs. 2.4.1-2), and some cannot (e.g., Fig. 2.2.6). The counterexample (Fig. 2.2.6) has a bridge, in fact it has three. Must every counterexample have a bridge? That is, can we say that every cubic graph which is connected and has no bridges can be decomposed into P3 subgraphs?
Do for discussion Mon. 3/11:
TEST I will be on Tuesday, Mar. 12. It will cover everything we've done so far (HW Sets I–VII).
For Fri. 3/15: Read Sections 4.1 and 4.2.
For Mon. 3/18: Read the handout on line graphs.
(This is not in the book. See the definition.)
Do for discussion Tues. 3/19:
Do for discussion Wed. 3/20:
Hand in Fri. 3/22:
H1. This question concerns the proof of Theorem 4.1.2* (that is, the base case k = 2 of Turan's Theorem). You are given the "starting" graph G of the proof, which has no triangle.
H2. The uniqueness of the maximum graph in Theorems 4.1.2* and 4.1.2 is not proved in the book.
For Fri. 3/22: Read Sects. 5.2-3 and the handout on the Matrix-Tree Theorem.
(Notice "for your own good".) The lectures on Fri. 3/22 and Tues. 4/2 are important. If you can teach yourself the material from the readings, you don't need to be there. Otherwise, be there.
Do for discussion Wed. 4/3:
Do for discussion Fri. 4/5:
Hand in Mon. 4/8:
Read:
Do for discussion Tues. 4/9:
Do for discussion Wed. 4/10:
Hand in Fri. 4/12:
Read Sects. 8.1-3. (This is a lot to discuss. Study carefully and come in Tuesday with many questions.)
Do for discussion Tues. 4/16:
Do for discussion Wed. 4/17:
Hand in Fri. 4/19:
TEST II will be on Tuesday, April 23. Monday before the test will be a review day.
Read Sects. 9.1-2. The proof of Theorem 9.1.7 is optional.
Do for discussion Mon. 4/29:
Do for discussion Tues. 4/30:
Do for discussion Wed. 5/1:
Hand in Fri. 5/3:
I1. Show that the graph of Fig. 9.1.16 is nonplanar.
I2. Planar or nonplanar? Prove it!
I3. Prove that cr(P) ≥ 2, where P is the Petersen graph. without using Theorem CR.
I4. (a) Prove that, if p ≥ 11, then Kp has no decomposition into two planar graphs.
I5. Do both (i) and (ii) for
(i) Is the graph planar?
I6. Write a complete proof of the 6-Color Theorem.
I7. (a) Prove Theorem G.
I8. Use Theorem G to do (a, b, d).
I9. (a) Prove Theorem CR.
I10. Use Theorem CR to solve:
Read: Sects. 9.3 and 10.3. (In 10.3, omit anything about "schemes", "maximal rotations", and "current graphs", and pp. 235-237.)
Do for discussion Tues. 5/7:
Hand in Wed. 5/8:
J1. Prove that cr(K6 − edge) = 2.
J2. Find θ(P), where P is the Petersen graph.
J3. Prove that θ(Kn) ≥ ceiling[(n+2)/6] for all n ≥ 1.
J4. Let c(G) = the number of cycles in the graph G.
J5. Let H = Heawood graph, Fig. 4.2.4.
J6. Find an easy proof that σ(P) ≥ 2, where P = Petersen graph. (Thus σ(P) = 2, by Exercise 9.3.4.)
J7. Try to embed non-planar complete graphs in the torus. Start with K5 (naturally), and if you succeed, try K6 and then K7 and then ....
J8. The same as # J7, for the double torus.
J9. Try to embed non-planar complete bipartite graphs in the torus. Start with K3,3 (naturally), and if you succeed, try K3,4 and then K3,5 and K4,4 – and then (we're getting into summer plans here) ....
Do for discussion Fri. 5/10:
K1. Let G be the Grötzsch graph (Fig. 2.1.6).
K2. Find χ'(Z) where Z is the graph of Fig. 2.3.1.
K3. Prove that K3,3 is the unique 4-cage.
K4. Compare the lower bound p(g) on the order of a g-cage (see Theorem 4.2.A) to the actual order of every known g-cage given in the book. Which cages have order equal to p(g)? Which have order greater than p(g)? What does it mean when a g-cage has order > p(g)?
Homework Set VII (2/24)
Sect. 2.4, ## 3, 10.
Sect. 3.2, ## 1-3, 8.
## G1(a), G2(a), G6, G7, G9(a), G10(a).
Sect. 2.4, ## 9 (Fig. 2.3.7), 12 (see correction), 21.
Sect. 3.1, ## 13, 14.
Sect. 3.2, ## 4, 6.
## G3(a), G4, G9(b), G10(b,c).
Sect. 2.4, # 22.
Sect. 3.1, ## 15, 16.
Sect. 3.2, ## 5.
## G1(b, c), G2(b, c), G3(b), G5, G8, G9(c), G10(d).
Problem Set G
(a) Fig. 1.2.3 (left).
(b) Fig. 2.1.9.
(c) Fig. 2.2.6 (right).
(a) Fig. 2.1.3.
(b) Fig. 2.4.1, the Petersen graph.
(b) Find a graph H which has a Hamilton cycle but no Eulerian circuit.
icosahedral dodecahedral graph I D in Fig. 1.2.5 [Egg on face: I is not cubic!],
Homework Set VIIa (3/6)
# G9(b) (corrected).
Go to homework index.Homework Set VIII (3/13, 16)
LG, ## 2, 3, 4.
Sect. 4.1, ## 1, 2, 4, 6.
Sect. 4.2, ## 2(a), 3.
# H1(a).
LG, # 9.
Sect. 4.1, ## 7, 8.
Sect. 4.2, ## 2(b), 4, 6.
# H2(a).
LG, ## 7, 10.
Sect. 4.1, ## 3, 5.
Sect. 4.2, ## 1, 2(c).
# H1(b).
Problem Set H
(i) Construct the new graph H in the proof of Theorem 4.1.2*. What are your x and W?
(ii) Compare the degrees of the vertices in G and H.
(iii) Compare qG and qH. Which is larger? Why is that significant for the proof of the theorem?
(iv) Compare H to the largest possible triangle-free graph on the same number of vertices. How are they similar?
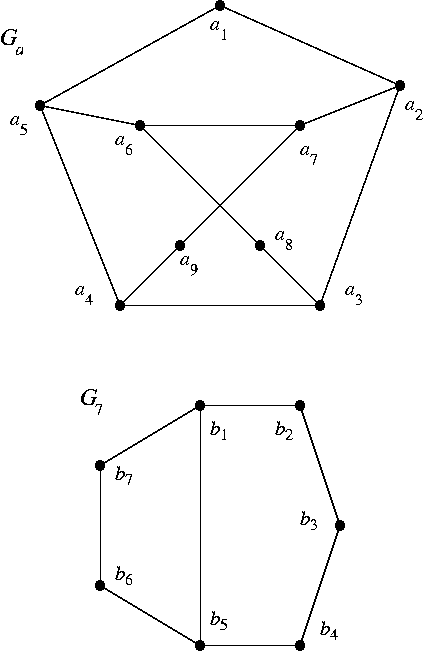
(a) For G = Ga, the Petersen graph with one vertex deleted. (See below.)
(b) For G = G7, shown below.
(a) Prove uniqueness in Theorem 4.1.2*.
(b) Prove uniqueness in Theorem 4.1.2.
Go to homework index.Homework Set IX (3/17, 19)
Problems from the Line Graphs handout are in the Version of March 18; that version gives the date in the heading.
Sect. 5.2, ## 1, 2, 3, 4(a), 5.
Sect. 5.3, ## 1, 4, 11(a).
MT, ## 1, 2.
LG, # 14 (in Version of 3/18).
Sect. 5.2, ## 8, 10.
Sect. 5.3, ## 3, 7(a), 10(left), 11(b,c).
MT, # 3.
Sect. 5.2, ## 4(b), 7, 9, 11.
Sect. 5.3, ## 2, 11(d).
MT, # 4.
LG, # 15 (in Version of 3/18).
Go to homework index.Homework Set X (3/25, 28)
Sects. 6.1, 7.1 for Mon. 4/8.
Sect. 6.1, ## 1-3, 5.
Sect. 7.1, ## 1(a), 2(left), 5.
Sect. 6.1, ## 6, 8, 10, 19.
Sect. 7.1, ## 3, 6.
Sect. 6.1, ## 7, 11, 21.
Sect. 7.1, ## 2(right).
Go to homework index.Homework Set XI (4/10)
Added: See Theorem 8.1.A on the relationship between maximal planar graphs and plane triangulations.
Sect. 8.1, ## 1-5, 7, 10.
Sect. 8.2, ## 3, 4.
Sect. 8.1, ## 8, 9, 12, 13.
Sect. 8.2, ## 1, 2.
Sect. 8.3, ## 2, 3.
Sect. 8.1, ## 6, 11.
Sect. 8.2, ## 5, 6.
Sect. 8.3, ## 4, 7.
Definition for Exercise 8.3.7
Go to homework index.Homework Set XII (4/24)
(The surprising thing about the proof of Theorem 9.1.6 is that it uses Turán's Theorem!)
Sect. 9.1, # 6.
## I1, I2(a), I3.
Sect. 9.1, ## 5, 14.
Sect. 9.2, ## 2, 3, 6.
## I2(b), I5(a), I8(a).
Sect. 9.1, ## 3, 4, 8, 12, 13.
Sect. 9.2, # 7.
## I4(a,b), I5(b).
Sect. 9.1, ## 1, 7, 11, 15.
Sect. 9.2, # 4.
## I2(c), I4(c), I5(c), I6, I7.
Corrections and Additions
d) no edge passes through any vertex;
e) whenever edges intersect, they cross.
See Theorem G, Theorem CR, and Theorem SPL, on the announcements page.
Problem Set I
(a) Fig. 9.1.19.
(b) Fig. 9.1.18.
(c) Fig. 9.1.17.
(d) Fig. 9.2.1, left.
(e) Fig. 9.2.1, right.
(b) Can K8 be decomposed into two planar graphs?
(c) Prove: if p ≥ 17, then Kp cannot be decomposed into three planar graphs.
(a) Fig. 2.3.6.
(b) Fig. 4.2.4.
(c) Fig. 1.3.3.
(ii) Find the crossing number. If you can't calculate it exactly, find out as much as you can about it. For instance, is it = 0 or > 0? Is it = 1? = 2? ≥ 2? ≥ 3? Can you find any upper bound?
(b) What does it say if g = 3?
(c) What does it say if G is bipartite?
(a) Prove: A cubic graph with girth g = 6 cannot be planar.
(b) Prove: A cubic graph with g ≥ 6 cannot be planar.
(c) Can a cubic graph with g = 5 be planar?
(d) Find a lower bound on cr(G) when G is cubic and has girth 6.
(b) What does it say if g = 3?
(c) What does it say if G is bipartite?
(a) Find cr(P), P = Petersen graph.
(b) Find cr(H), H = Heawood graph (Fig. 4.2.4).
Go to homework index.Homework Set XIII (5/1)
Be sure to study the Supplement to Section 10.3 on the announcements page.
Sect. 10.3, ## 1, 8, 9.
## J2, J3, J5, J7, J8, J9.
Sect. 10.3, ## 7, 10.
# I9 (added).
## J1 cancelled, J4, J6.
Definition
Problem Set J
(a) Prove Theorem M: If c(G) < min(c(K5), c(K3,3)), then G is planar. (Hint: Use Kuratowski's theorem.)
(b) Evaluate the minimum in Theorem M.
(c) Use (b) to solve Exercise 8.1.3. (If you didn't solve (b), just prove the minimum in (b) is > 3; that should be enough for Exercise 8.1.3.)
(a) Prove σ(H) ≥ 2.
(b) We know σ(H) ≤ 3. Decide whether σ(H) = 2 or 3.
Use theorems in Section 10.3 to decide where to stop embedding in the double torus.
Use theorems in Section 10.3 to decide where to stop embedding in the torus.
Go to homework index.Homework Set XIV (5/1)
Problem Set K (review problems).
Problem Set K
(a) Prove χ(G) = 4.
(b) Is G critical?
Go to homework index | announcements | course information | syllabus.