The homework advice page has advice about how graph theory problems should be done, not entirely the same as problems in other 300-level math courses.
We use class time on Wednesdays (and possibly Thursdays) for class discussion of graph theory, including homework problems and questions about the text or anything else.
Important homework rule: In solving homework problems, you are not allowed to justify your answer by appeal to anything you find outside our book, or to anything in the book that's ahead of the readings we've done.
Boldface problems were graded. Other problems were not graded.
This assignment is for discussion in class (except "Hand In"). Come up with IDEAS and bring them all along!

Due Wed., 2/17:
Read Section 1.1.
Also, read the course information page and the homework instructions.
Do for discussion on Wed. and Thurs., 2/17-18 (not to hand in):
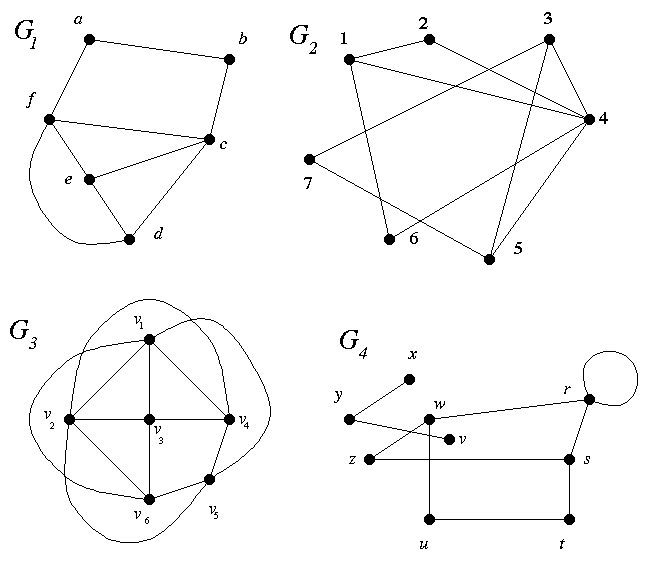
## A1–A5 for G = G1 and G2.
Hand in Sat. 2/20, 3:00 p.m.:
## A1–A5 for G3, G4.
Some terminology about a graph (from the announcements page):
A1. (a) Find a separating set. (b) Find one that is smallest.
A2. (a) Find a disconnecting set. (b) Find one that is smallest.
A3. Write down the degree sequence.
A4. Treat G as a graph in which the vertices stand for people and the edges join pairs who don't get along together, so they can't be on the same committee. What is the largest possible committee?
A5. Is the graph planar, i.e., can you draw it in the plane without crossings?
Due Thurs., 2/18:
Read Section 1.2.
Due Fri., 2/19:
Read Section 1.3 and the automorphisms handout.
Due for discussion Wed., 2/24:
Do for discussion Thurs. 2/25:
Hand in B1. This problem concerns ways of testing graphs for being isomorphic or nonisomorphic. In each part, suppose G and H are isomorphic graphs.
The point is that, if G and H are graphs that fail any one of these properties, then they cannot be isomorphic (by contradiction). But the converse is not true, as the next problem shows.
B2. For each property in # 1, find a pair of graphs, G and H, that are not isomorphic but which have the property. Specifically:
C1. This concerns Theorem 1.1.2 and the example G0. I follow the book's notation.
The sequence
C2. In the graph F of Figure 1.1.16:
C3. Let G be a graph which has a cycle. Let C be a cycle in G. Let a, b be arbitrary vertices in G, and let e be any edge in C. Explain in detail why, if G has a path connecting a to b, so does G − e.
Homework Set II (2/17)
Remember to check the announcements page for corrections to the textbook.
## B1(c), B2(c) (think about them for a few minutes; we'll discuss them in class).
Sect. 1.1, ## 1, 2, 4(a-c), 6.
Sect. 1.2, # 1, 4, 7.
Sect. 1.1, # 9.
Sect. 1.2, ## 2, 3, 6, 8.
# C2.
Sat., 2/27 Sun., 2/28, 3:00 p.m. (by email in PDF format):
## B1(a,b), B2(a,b).
Sect. 1.1, ## 3, 4(d), 5, 7, 8.
Sect. 1.2, # 5.
## C1, C3.
Problem Set B
Problem Set C
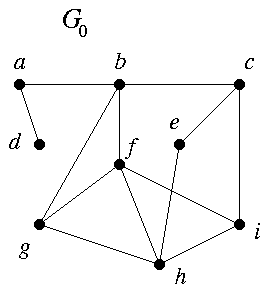
(S1) (4, 4, 4, 3, 3, 3, 2, 2, 1)
is known to be graphic, because it is the degree sequence of G0. From (S1) the rule of Theorem 1.1.2 gives
(S2) (3,3,2,2,3,2,2,1),
which, when rearranged in descending order, is
(S3) (3,3,3,2,2,2,2,1).
Go to homework index.
For Fri. 2/26: Read the extra theorems for Section 1.3. I also posted some basic graph-theory counting formulas.
Starting with HW III, I will give 4 bonus points for Latex homework.
For Mon. 3/1: Read Section 2.1.
Do for discussion Wed. 3/3:
Do for discussion Thurs. 3/4:
Hand in Sun. 3/7 by 3:00 p.m.:
In general (see homework advice), you should start on our homework well ahead of the due date, because some of the problems are easy but some take a lot of thought, which is best done in pieces, even on successive days. That's particularly true in this set.
Homework Set III (2/24)
Sect. 2.1, ## 1-4, 8, 13, 18, and 9-10 (for P5, K4,4, D, and O).
## D1, D4.
Sect. 2.1, ## 6, 11, 14, 16, 17.
# D5.
Sect. 2.1, ## 5, 7, 15(a), 19, 20 (see announcement), and 9-10 (for I).
## D2, D3, D6, D7(ab),(c),(d).
Textbook Corrections
Always remember to check the announcements page for corrections! There are several others for this section.
D1. Suppose G is a connected graph whose average degree is > 2. (Hint: See page 19.) Prove that it is possible for G to have exactly 2 cycles.
D2. Suppose G is a connected graph whose average degree is 3. (Hint: Use a similar idea to D1, but you have to add something.)
(a) Show that G has at least 4 cycles.
(b) Is 4 the best possible number? Or can you prove that G must have 5 or more cycles? 6 or more?
D3. Here are some theorems that characterize two important kinds of graph. See what you can do. (a) may be a mistake (I don't know myself). (b) is true.
D4. Find the chromatic number χ(G) where G is the graph in Figure 2.1.5.
D5. Is the graph of Figure 2.1.5 critical? Prove. (Don't believe everything you read!)
D6. Is the graph of Figure 2.1.6 critical? Prove.
D7. Find all critical graphs with chromatic number
For Thurs. 3/11: Read Sections 2.2, 2.3 and the line graphs handout.
Do for discussion Thurs. 3/11:
Do for discussion Fri. 3/12:
Hand in Homework Set IV (3/9)
Sect. 2.2, ## 3, 5, 6.
Sect. 2.3, ## 1-3.
## E1(a), E5(a), E7(a,b).
Sect. 2.2, ## 8, 9.
Sect. 2.3, ## 4, 5-7 (for Q3 and I), 8, 10, 12.
## E5(b,c), E7(c), E8-9(a-c).
Mon. 3/15 Tues. 3/16 (any time, even after midnight):
Sect. 2.2, ## 4, 7, 10.
Sect. 2.3, ## 5-7 (for D), 17.
## E1(b), E2, E5(d), E6, E7(d), E8(d), E9(c).
Textbook Corrections
E1. Prove there is no 1-factor in the graph of Figure 2.2.6 (a) left, (b) right.
E2. Is the graph of Figure 2.1.2 critical? Prove.
The first example graph theorists look at when they have a complicated new idea is Kp. The next one could be Kp − edge.
E3. Let G = Kp − edge. Find the chromatic number χ(G).
E4. Let G = Kp − edge. Find the edge chromatic number χ'(G) when p is even, i.e., p = 2n (n ≥ 1). How does it compare to the maximum degree Δ(G)?
E5. Let V(K2n) = {0, 1, 2, ..., 2n−2, x}. We have a standard way to decompose K2n into 1-factors (see Section 2.2). In K8, which "standard" 1-factor contains the following edge? (For your answer you may list all edges that belong to the 1-factor.)
(a) 23.
(b) 2x.
(c) 36.
(d) 15.
E6. Prove that, if G is a tree, then its edge chromatic number χ'(G) equals its maximum degree Δ(G).
E7. Find a Hamilton cycle or prove there is none.
(a) Figure 2.3.4.
(b) Figure 2.3.5. (Hint: there isn't!)
(c) Figure 2.1.6.
(d) Figure 2.3.7.
E8. Find the line graph of each graph.
(a) Pn for n ≥ 1.
(b) Cn for n ≥ 3.
(c) K4.
(d) K4 − edge.
E9. Is the line graph regular? If so, what is the degree (i.e, the degree of each vertex)?
(a) Pn for n ≥ 1.
(b) Cn for n ≥ 3.
(c) Kn for n ≥ 4.
Read Sections 2.4, 3.1. (The proofs in 3.1 show you how to construct trails, decompositions, etc.)
"Quiz" means this question is likely to be on an in-class, open-book quiz.
Campus notice: No classes on Wed. 3/17! It's Rejuvenation Day.
Recommendation: To understand the 4-dimensional cube (or "tesseract"), read the short story "—And He Built a Crooked House".
Do for discussion Thurs. 3/18:
Do for discussion Fri. 3/19:
Hand in Homework Set V (3/13)
Sect. 2.3, # 18(a).
Sect. 2.4, ## 1, 4, 10.
Sect. 3.1, ## 1-3, 4 (for Q3, K4,4 only), 7 (quiz).
## F3(a), F4(a), F8(a), F9.
Sect. 2.3, ## 18(b).
Sect. 2.4, ## 2, 8, 12 (see correction).
Sect. 3.1, ## 5, 8, 11, 13.
## F1(a,b), F5(a), F6, F7(a), F8(b) (quiz).
Tues. 3/23 | Thurs. 3/25 Fri. 3/26 (any time of day or night):
Sect. 2.3, # 18(c).
Sect. 2.4, # 7, 22, 25.
Sect. 3.1, ## 6, 12, 14.
## F1(d), F2, F3(b,c), F4(b,c), F5(b), F8(d), F10.
Textbook Corrections
F1. Let V(K2n+1) = {0, 1, 2, ..., 2n-1, x}. We have a standard way of decomposing K2n+1 into Hamilton cycles (see Section 2.3). In K11, which "standard" Hamilton cycle contains the edge
(a) 23 ?
(b) 3x ?
(c) 46 ?
(d) 37 ?
F2. We define a graph to be connected if for any two vertices, there is a path between them (page 17). A fundamental fact is that, if there is a walk between vertices u and v, then there is a path between them (see Connection Theorem). Prove this. (It is possible that the proof of C3 may suggest an idea.)
F3. Decompose into the fewest possible trails:
(a) Fig. 1.2.3 (left).
(b) Fig. 2.1.9.
(c) Fig. 2.2.6 (right).
F4. Decompose into the fewest possible paths: (a, b, c) from #F3.
F5. Decide whether the graph is Hamiltonian (i.e., has a Hamilton cycle):
(a) Fig. 2.1.3.
(b) Fig. 2.4.1, the Petersen graph.
F6. Verify that, in the proof of Theorem 2.3.2, the first two 1-factors unite to form a Hamilton cycle. Your proof should be valid for all n ≥ 2.
F7. Regarding tree decompositions of Kp as mentioned at the bottom of page 39:
F8. Use the proof method of Theorem 3.1.7 (Listing's Theorem) to decompose into the smallest possible number of trails:
F9. (a) Find a graph E which has an Eulerian circuit but no Hamilton cycle.
(b) Find a graph H which has a Hamilton cycle but no Eulerian circuit.
F10. (Bonus problem.) Exercise 2.4.14 asks you to decompose the Petersen graph into 3 subgraphs isomorphic to each other, that is, they are all isomorphic to some graph H. The bonus question is: How many nonisomorphic graphs H are there, for which this is possible? Each must have 5 edges, since Petersen has 15 edges. This is an open-ended question; see how many H's you can come up with.
For Thurs. 3/25 read Section 3.2. For Fri. 3/26 read Sections 4.1 and 4.2. (We won't do much with 4.2. Get the general impression.) For Mon. 3/29 read Section 3.3.
For Mon. 3/29: Read the handout "LG" on line graphs.
(This is not in the book. See the definition.) For the complement of a graph see the definition.
Do for discussion Wed. 3/31:
Do for discussion Thurs. 4/1 (ha ha! Didn't fool you!):
Hand in Mon. 4/5 (any time) (not due Easter Sunday):
H1. This question concerns the proof of Theorem 4.1.2* (that is, the base case k = 2 of Turan's Theorem). You are given the "starting" graph G of the proof, which has no triangle.
H2. The uniqueness of the maximum graph in Theorems 4.1.2* and 4.1.2 is not proved in the book.
Homework Set VI (3/22, 25)
LG, ## 2, 3.
Sect. 1.3, ## 1, 2, 6.
Sect. 3.2, ## 1-3.
Sect. 3.3, ## 1, 4, 5.
Sect. 4.1, ## 1, 2.
Sect. 4.2, ## 2(a).
# H1(a).
LG, # 9.
Sect. 1.3, ## 11, 14.
Sect. 3.2, # 4.
Sect. 3.3, # 17 (see correction).
Sect. 4.1, ## 4, 6, 7.
Sect. 4.2, ## 2(b).
# H2(a).
LG, ## 7, 10.
Sect. 1.3, ## 7, 10.
Sect. 3.1, ## 15, 16.
Sect. 3.2, # 8.
Sect. 4.1, ## 3, 5.
Sect. 4.2, # 2(c), 3, 6.
# H1(b).
Problem Set H
(i) Construct the new graph H in the proof of Theorem 4.1.2*. What are your x and W?
(ii) Compare the degrees of the vertices in G and H.
(iii) Compare qG and qH. Which is larger? Why is that significant for the proof of the theorem?
(iv) Compare H to the largest possible triangle-free graph on the same number of vertices. How are they similar?
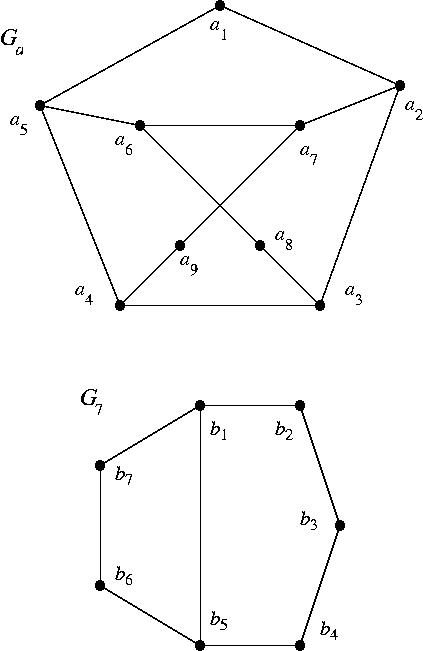
(a) For G = Ga, the Petersen graph with one vertex deleted. (See below.)
(b) For G = G7, shown below.
(a) Prove uniqueness in Theorem 4.1.2*.
(b) Prove uniqueness in Theorem 4.1.2.
Go to homework index.
For Thurs. 4/1: Read Sect. 5.1 (omit the material on derangements and the numbers Dn).
Do for discussion Mon. 4/5:
Do for discussion Wed. 4/7:
Hand in Thurs. 4/8 (there is no class this day!) by 1:00 p.m. so I can return it by Friday's class:
Homework Set VII (3/31)
For Fri. 4/2: Read Sect. 5.2.
Sect. 5.2, ## 1, 2, 3, 4(a), 5.
LG, # 14.
Sect. 5.2, ## 8, 10.
Sect. 5.2, ## 4(b), 7, 9, 11.
LG, # 15.
Go to homework index.
Midterm exam: April 12–13.
For Thurs. 4/15: Read Sect. 5.3 and the handout on the Matrix-Tree Theorem.
For Fri. 4/16: Read Sect. 6.1.
Do for discussion Fri. 4/16:
Sect. 5.3, ## 3, 4,7(a), 11(a).
Hand in Mon. 4/19:
Sect. 5.3, ## 1, 2.
Read for Mon. 4/19: Sects. 6.2, 7.1. Check the announcements page for the incidence matrix.
Do for discussion Wed. 4/21:
Do for discussion Thurs. 4/22:
Hand in Mon. 4/26 (not Fri. 4/23) by Voluntary bonus Challenge Problems, due any time before the final exam:
I1. Suppose G is a connected digraph with p vertices. Prove that the rank of the incidence matrix M(G) equals p − 1. (See the announcements page for hints.)
I2. Suppose G is a strongly conservative digraph. Then there is an edge labelling f using the numbers 1, 2, ..., q, once each, such that f satisfies Kirchhoff's Current Law (KCL) and also for every integer h, the labelling f+h satisfies KCL. Remember that f+h is the labelling that assigns edge e the label f(e)+h.
I3. Suppose G is a strongly conservative digraph. Then for every vertex v, the number of edges with head at v = the number of edges with tail at v. (Hint: Use #I2.)
I4. The proof that K3,3 is nonconservative that we worked out in class on 4/21, based on Alex's suggestion, suggested possible generalizations that could use the same idea.
Homework Set IX (4/14, 16, 19)
Sect. 6.1, ## 1-3, 5.
Sect. 6.2, ## 1, 5.
Sect. 7.1, ## 1(a), 2(left), 5.
Sect. 6.1, ## 6, 8, 10, 19.
Sect. 6.2, ## 6, 9.
Sect. 7.1, ## 3, 6.
6:00 p.m. any time:
Sect. 6.1, ## 7, 11, 21(a,b,c).
Sect. 6.2, ## 7, 10, 12, 14.
Sect. 7.1, ## 2(right).
## I1, I2 (optional), I3 (optional).
# I4, any parts.
Problem Set I
Go to homework index.
Read for Mon. 4/26: Sects. 8.1-3. (This is a lot to discuss. Study carefully and come in with many questions.)
Do for discussion Wed. 4/28:
Do for discussion Thurs. 4/29:
Do for discussion Fri. 4/30:
Hand in J1. (a) Prove that, if p ≥ 11, then Kp has no decomposition into two planar graphs.
J2. Write a complete proof of the 6-Color Theorem.
J3. (a) Prove Theorem G.
J4. Use Theorem G to do (a, b).
Homework Set X (4/14, 26)
See Theorem 8.1.A on the relationship between maximal planar graphs and plane triangulations.
Sect. 8.1, ## 1-5, 7, 10.
## J4(a).
Sect. 8.1, ## 8, 9, 12, 13.
Sect. 8.2, ## 1, 2.
## J1(a,b).
Sect. 8.2, ## 3, 4.
Sect. 8.3, ## 2, 3.
Fri. 4/30 Mon. 5/3 before class:
Sect. 8.1, # 11.
Sect. 8.2, ## 5, 6.
Sect. 8.3, ## 4, 7.
## J1(c), J2, J3, J4(b-c).
Corrections and Additions
See Theorem G on the announcements page.
Problem Set J
(b) Can K8 be decomposed into two planar graphs?
(c) Prove: if p ≥ 17, then Kp cannot be decomposed into three planar graphs.
(b) What does it say if g = 3?
(c) What does it say if G is bipartite?
(a) Prove: A cubic graph with girth g = 6 cannot be planar.
(b) Prove: A cubic graph with g ≥ 6 cannot be planar.
(c) Can a cubic graph with g = 5 be planar?
Go to homework index.
Read Sections 9.1 and 9.2. The proof of Theorem 9.1.7 is optional.
Do for discussion Wed. 5/5:
Do for discussion Thurs. 5/6:
Do for discussion Fri. 5/7:
Hand in Mon. 5/10 before class:
K1. Show that the graph of Fig. 9.1.16 is nonplanar.
K2. Planar or nonplanar? Prove it!
K3. Prove that cr(P) ≥ 2, where P is the Petersen graph, without using Theorem CR.
K4. Use Theorem CR to solve:
K5. Do both (i) and (ii) for
(i) Is the graph planar?
K6. Write a complete proof of the 4-Color Theorem for Triangle-Free Graphs.
K7. (a) Prove Theorem CR.
K8. Use Theorem G to find a lower bound on cr(G) when G is cubic and has girth 6.
Homework Set XI (5/3)
The surprising thing about the proof of Theorem 9.1.6 is that it uses Turán's Theorem!
Sect. 9.1, # 6.
## K1, K3, K4(a).
Sect. 9.1, ## 5, 14.
Sect. 9.2, ## 2, 6.
## K2(a,b), K5(a).
Sect. 9.1, ## 3, 4, 12, 13.
Sect. 9.2, ## 3, 7.
## K5(b), K8.
Sect. 9.1, ## 1, 7, 11, 15.
Sect. 9.2, ## 3, 4.
## K2(c), K4(b), K5(c), K6, K7.
Corrections and Additions
d) no edge passes through any vertex;
e) whenever edges intersect, they cross.
See Theorem CR and Theorem SPL on the announcements page.
Problem Set K
(a) Fig. 9.1.19.
(b) Fig. 9.1.18.
(c) Fig. 9.1.17.
(d) Fig. 9.2.1, left.
(e) Fig. 9.2.1, right.
(a) Find cr(P), P = Petersen graph. Is it easier than #K3?
(b) Find cr(H), H = Heawood graph (Fig. 4.2.4).
(a) Fig. 2.3.6.
(b) Fig. 4.2.4.
(c) Fig. 1.3.3.
(ii) Find the crossing number. If you can't calculate it exactly, find out as much as you can about it. For instance, is it = 0 or > 0? Is it = 1? = 2? ≥ 2? ≥ 3? Can you find any upper bound?
(b) What does it say if g = 3?
(c) What does it say if G is bipartite?
Go to homework index.
Read: Sects. 9.3 (for Wed. 5/12; you already saw most of this in class) and 10.3 (for Thurs. 5/13). (In 10.3 omit anything about "schemes", "maximal rotations", and "current graphs", and pp. 235-237.)
Do for discussion Thurs. 5/13 and Fri. 5/14:
Hand in Sun. 5/16:
L1. Prove that cr(K6 − edge) = 2.
L2. Find θ(P), where P is the Petersen graph.
L3. Prove that θ(Kn) ≥ ceiling[(n+2)/6] for all n ≥ 1.
L4. Let c(G) = the number of cycles in the graph G.
L5. Let H = Heawood graph, Fig. 4.2.4.
L6. Find an easy proof that σ(P) ≥ 2, where P = Petersen graph. (Thus σ(P) = 2, by Exercise 9.3.4.)
L7. Try to embed non-planar complete graphs in the torus. Start with K5 (naturally), and if you succeed, try K6 and then K7 and then ....
L8. The same as # L7, for the double torus.
L9. Try to embed non-planar complete bipartite graphs in the torus. Start with K3,3 (naturally), and if you succeed, try K3,4 and then K3,5 and K4,4 – and then (we're getting into summer plans here) ....
Homework Set XII (5/11)
Be sure to study the Supplement to Section 10.3 on the announcements page.
Sect. 9.3, ## 3, 13.
Sect. 10.3, ## 1, 8, 9.
## L2, L3, L5, L7, L8.
Sect. 9.3, ## 1, 4.
Sect. 10.3, ## 7, 10.
## L4, L6, L9.
Definition
Problem Set L
(a) Prove Theorem M: If c(G) < min(c(K5), c(K3,3)), then G is planar. (Hint: Use Kuratowski's theorem.)
(b) Evaluate the minimum in Theorem M. If you can't find the exact minimum, just prove it is > 3.
(c) Use (b) to solve Exercise 8.1.3.
(a) Prove σ(H) ≥ 2.
(b) We know σ(H) ≤ 3. Decide whether σ(H) = 2 or 3.
Use theorems in Section 10.3 to decide where to stop embedding in the double torus.
Use theorems in Section 10.3 to decide where to stop embedding in the torus.
Go to homework index.
Do for discussion Mon. 5/17:
Hand in Tues. 5/18:
M1. Let G be the Grötzsch graph (Fig. 2.1.6).
M2. Find χ'(Z) where Z is the graph of Fig. 2.3.1.
M3. Prove that K3,3 is the unique 4-cage.
M4. Prove Theorem 4.2.A.
M5. Compare the lower bound p(g) on the order of a g-cage (Theorem 4.2.A) to the actual order of every known g-cage given in the book. Which cages have order equal to p(g)? Which have order greater than p(g)? What does it mean when a g-cage has order > p(g)?
M6. I'll define a graph R. V(R) is the set of all unordered pairs ij of elements of the set S5 = {1, 2, 3, 4, 5}. (I use the simplified notation ij to mean the set {i, j}.) The pair {ij, kl} is an edge when i, j, k, l are four distinct elements of S5.
Homework Set XIII (5/11)
M1, M4, M5, M6 (especially valuable).
M2, M3.
Problem Set M (review problems)
(a) Prove χ(G) = 4.
(b) Is G critical?
(a) Prove that R is isomorphic to the Petersen graph, P.
(In fact, this is one way to define the Petersen graph. From now on I will call this graph P, as there is no difference.)
(b) Prove that P is the complement of the line graph of K5.
(c) Prove that for every two edges in P, say e and e', there is an automorphism f of P such that f(e) = e'.
(This fact is useful in problems like #K3, because all edges can be treated at once instead of in three cases.)
Go to homework index | announcements | course information | syllabus | syllabus + recordings.