Matroid Theory Assignments:
Readings and Problems

Hand-In Assignments

Written work: Your choices must be approved in advance by me. (This is to make sure they aren't too easy or too hard.)

Extra Problems

Extra problems on duality: PostScript file.

Extra problems on projective geometry (Section 6.1). (The most important is the second one.)

1. Practice with projective geometries. (Very important.) The problem is for q = 5. (q = 4 is also very interesting but harder.)
   • (a) Write down all the equivalence classes that are the points of PG(1,5). This means: write down names of the equivalence classes (these are in brackets []) and write down all the elements of each equivalence class (these are vectors in GF(5)^2 and are written with parentheses ()).
   • (b) Look for a pattern that lets you write down names of all the equivalence classes easily.
   • (b) Write down names of all the equivalence classes that are the points of PG(2,5). Again, look for a pattern that makes it easy. Your pattern should make it easy to see that there are q^2 + q^1 + q^0 points.
   • (c) Find equations of the ``ordinary'' (or ``affine'') lines in PG(2,5). (This means the lines that are not the ideal line.) Do you see a pattern in the equations? (You do not need to do all the lines, but do at least 10 of them.)
   • (d) Each ordinary line contains a single ideal point. Find the equation of that ideal point, for several of the ordinary lines you studied in (c).
   
   
2. Make sure you can prove that a coordinatizable projective geometry satisfies the modular law. If ambitious, prove the modular law for projective planes in general (thus it will be proved for all projective geometries, by the coordinatization theorem).
   
   
3. A subset S of a matroid M is line-closed if, whenever x,y in S, then cl({x,y}) is contained in S.
   • (a) Prove that any flat in a matroid is line closed.
   • (b) Prove that, in a coordinatizable projective geometry, any line-closed set is a flat. (Recall that we define the matroid of such a PG as the simplification of a vector matroid.)
   • (c) Prove by counterexample(s) that (b) is not true of matroids in general.
   The point of this problem is that it tells you a simple way to know which point sets in an abstract projective geometry are flats.
   
   
4. In PG(n-1,q), the number of complements of a rank-k flat is equal to q^k(n-k). (Prove.)

Extra problems on the Möbius function.

1. In connection with the incidence algebra of a poset P, prove:
   • (a) * is associative;
   • (b) delta is the identity;
   • (c) mu is a left inverse of zeta and is the only one.
2. Prove that the characteristic polynomial of any matroid (except of rank 0) has a factor (lambda - 1).
3. Don't overlook problems that consist of proofs that are left as exercises. In particular, you should do at least one of the proof exercises (8-12) and you should try at least two of them.

Extra problems on hyperplane arrangements.

1. Show that in the matroid of a hyperplane arrangement H, the rank function is r(S) = codim(intersection of S), for any S subset of H.
2. Show that if h is in H, then M(H_h) (the matroid of the arrangement induced in h) = M(H)/h.

Problems on gain and biased graphs.
^* means an advanced problem.

1. First set of problems on gain and biased graphs.
   1. ^* Prove the theorem that a biased graph Omega is the biased graph of a signed graph if and only if Omega contains no contrabalanced theta graph.
   2. Draw the hyperplane arrangement corresponding to the signed graph ±K₂ (the signed expansion of K₂).
   3. Draw the group expansion Z₃·K₃ . List all the balanced circles. Is this gain graph balanced? Be specific.
   4. Make up a signed graph: not too large, about 8-12 edges, and with a few circles; make it connected and an ordinary graph. Decide whether or not it is balanced. Be specific. Solve by at least two different methods, one of them being switching.
   5. Problems on varying the gain group. Suppose Phi is a gain graph.
      1. If the gain group is not generated by the edge gains, how can you (in a very simple way) make a gain graph that has the same bias but a smaller gain group?
      2. If the gain group is generated by the edge gains but not by the circle gains, how can you (in a simple way) make a gain graph that has the same bias but a smaller gain group?
   6. ^* More problems on varying the gain group. Interpret the question as asking about isomorphism types of gain graphs, not individual gain graphs.
      1. Draw the group expansion ±K₂ . Find all gain graphs Phi such that <Phi> = <±K₂> and the gain group of Phi is generated by the circle gains. (Think about the use of switching.)
      2. The same, but with ±K₃ .
      3. The same, but with Z₃·K₃ .
      4. The same, but with GK₃ where G is any group. What conclusion can you draw, from your results, about GK_n ?
   7. Prove the theorem that, for a gain graph Phi, <Phi>/S = <Phi/S>. Write a complete proof.
   
   
2. Second set of problems on gain and biased graphs.
   1. Write a detailed proof that switching does not change the list of balanced circles of a gain graph.
   2. This problem refers to gain graph GG₁ .
      1. Decide whether the gain graph is balanced.
      2. Classify the edges into balanced and unbalanced.
      3. Switch the gains so that the spanning tree of your choice has gains all equal to the identity (0, in this case).
      4. Find the balance-closure of {e, vw, vy, tx, tu, ss}. (e is one of the qw edges.)
      5. Find the bias-matroid closure clos_G(S), where S is:
         1. {e, vw, vy, tx, tu, ss},
         2. {e, vw, ry, tx, tu, ux, ss},
         3. {pr, py, e, vw, vy, tx, tu, ss},
         4. {h_r , pr, py, e, ss, st} (h_r is the half edge at r),
         5. {h_r , ps, pr, py, e}.
      6. Contract S to get a new gain graph, where S is:
         1. {e, vw, vy, tx, tu},
         2. {e, vw, ry, tx, tu, ux},
         3. {h_r},
         4. {e, vw, ry, tx, tu, ux, ss},
         5. {ps, py, sy, uv, vw, wx},
         6. {h_r , py, e, vw, ry, tx, tu, ux}.
      7. Prove that G(Phi/S) = G(Phi)/S for one or two small sets S in the previous part. Try to find a general way of thinking that could be developed into a general proof.
         

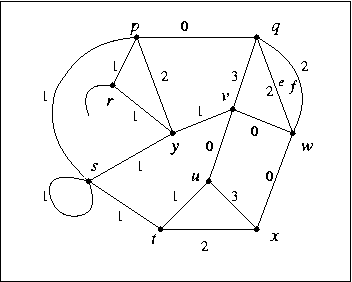
         Gain Graph GG1. The gain group is Z4 . The gains on the diagram should be read in alphabetical order (from the "lower" to the "higher" letter). The funny-looking symbol that resembles "L" is 1.

         Here is a PostScript version of the figure that prints nicely.
         
         
   3. Prove the theorem that G(Omega)/S = G(Omega/S).
   4. Fix up the details of the proof that bcl(S) is balanced if S is balanced, for a biased graph. You should look up Tutte's Path Theorem to verify that you are using the correct statement. (Looking it up is part of this exercise.)
   5. Work out your own proof that, in a biased graph, bcl(bcl(S)) = bcl(S) if S is balanced.
   6. Find the bias matroid of the gain graph. Make an affine diagram. Identify it as a familiar matroid, if possible.
      1. ±K₃ ,
      2. ±K₃ with one unbalanced edge,
      3. Z₃·K₃ ,
      4. -W₄ , the 4-spoke wheel with all edges negative,
      5. -K₄ ,
      6. ^* -K₅ with one edge deleted.
   7. Prove directly from the definitions:
      1. The bias circuits of a biased graph are the circuits of a matroid.
      2. The rank function r_G of the bias matroid is a matroid rank function.
   
   
3. Third set of problems on gain and biased graphs: lift matroids.
   1. This problem refers to gain graph GG₁.
      1. Find the lift-matroid closure clos_L(S), where S is:
         1. {e, vw, vy, tx, tu, ss},
         2. {e, vw, ry, tx, tu, ux, ss},
         3. {pr, py, e, vw, vy, tx, tu, ss},
         4. {h_r, pr, py, e, ss, st},
         5. {h_r, ps, pr, py, e}.
      2. Decide whether or not L(Phi/S) = L(Phi)/S for one or two small sets S in the previous part.
   2. Consider the equation L(Omega)/S = L(Omega/S).
      1. Prove that it holds if S is balanced.
      2. Prove that equality need not hold if S is not balanced.
      3. Can equality hold if S is balanced?
   3. Produce an example of a 2-connected biased graph (you may use a gain graph, of course) for which the bias and lift matroids are different.
   4. Find the lift and complete lift matroids of the gain graph. Make an affine diagram. Identify the matroid, if possible.
      1. ±K₃ ,
      2. ±K₃ with one unbalanced edge,
      3. -W₄ ,
      4. -K₄ .
   5. Prove (a) and (b) directly from the definitions:
      1. The lift circuits of a biased graph are the circuits of a matroid.
      2. The rank function r_L of the lift matroid is a matroid rank function.
      3. Deduce from (b) that the rank function r_L0 of the complete lift matroid is a matroid rank function.
   
   
4. Fourth set of problems on biased graphs: finding the graph.
   
   A matroid M is a minor-minimal nonbias matroid (or a forbidden minor for bias matroids) if M is not the bias matroid of any biased graph, but every proper minor of M is the bias matroid of some biased graph.
   A matroid M is a a forbidden minor for lift matroids of biased graphs if M is not the lift matroid of any biased graph, but every proper minor of M is the lift matroid of some biased graph.
   1. Find all biased graphs Omega (without isolated vertices) such that G(Omega), the bias matroid, is the specified matroid:
      1. The m-point line, L_m = U_2,m , for each m >= 3.
      2. The m-point circuit, U_m-1,m .
      3. The uniform matroid U_3,m , for m = 4, 5, 6, 7.
      4. * The uniform matroid U_4,7 .
      5. Is any of these a minor-minimal nonbias matroid?
   2. Find all biased graphs Omega (without isolated vertices) such that L(Omega), the lift matroid, is the specified matroid:
      1. The m-point line, L_m , for each m >= 3.
      2. The m-point circuit, U_m-1,m .
      3. The uniform matroid U_3,m , for m = 4, 5, 6, 7.
      4. * Is any of these a forbidden minor for lift matroids of biased graphs? Can you make use of them to find such a forbidden minor?
   3. Show that F₇ is not the bias matroid of any biased graph. Furthermore, every proper minor of F₇ is a bias matroid of a biased graph (thus, F₇ is a minor-minimal nonbias matroid).
   4. * The same for the dual matroid, F₇*.
   5. * Find a biased graph Omega of which the non-Fano matroid F₇^- is the bias matroid. If you can, find all such biased graphs.
   6. Find a simple necessary and sufficient condition on a biased graph for its bias and lift matroids to be equal.
   
   
5. Problems on representations of biased graphic matroids.
   
   These problems refer to the following list of biased graphs:
   1. (2K₂, nullset) ,
   2. <±K₃> ,
   3. <Z₃·K₃> ,
   4. <-W₄> .
   1. Decide whether the biased graph has gains in the following groups: Q*, R*, C*, Q⁺, R⁺, C⁺.
   2. Decide whether the biased graph has a canonical bias representation over the following fields: Q, R, C.
   3. Decide whether the biased graph has a canonical lift representation over the following fields: Q, R, C.
   4. * For each biased graph in ## 2 and 3 that does have a canonical bias or lift representation, does it have a unique such representation (as always, that means up to projective equivalence)?
   5. * Does the biased graph have a noncanonical representation over any of the following fields: R, C ? Here by ``noncanonical'' I mean a representation that is not projectively equivalent to any canonical representation.