The homework advice page has advice about how graph theory problems should be done, not entirely the same as problems in other 300-level math courses.
We use some class time for discussing graph theory, including homework problems and questions about the text or anything else.
Important homework rule: In solving homework problems, you are not allowed to justify your answer by appeal to anything you find outside our book, or to anything in the book that's ahead of the readings we've done.
Boldface problems were graded. Other problems were not graded.
§ means "section".
(corr) means correction (with a link to the correction on the announcements page).
Read Section 1.1 for Fri., 1/24.
Also, read the course information page and the homework instructions.
Hand in Mon. 1/27:
§ 1.1, # 4.
Read Section 1.2 for Mon.-Wed., 1/27-29.
Do for discussion on Wed. 1/29 (not to hand in):
§ 1.1, # 2a; § 1.2, ## 2, 7.
Hand in Fri. 1/31:
§ 1.1, ## 1, 2b, 5, 7 (see correction).
§ 1.2, ## 1, 3, 5, 6, 9.
For the class discussion, come up with ANY IDEAS and bring them along!

Due Wed., 2/5:
Read Section 1.3 for Mon., 2/3.
Do for discussion on Wed., 2/5 (not to hand in):
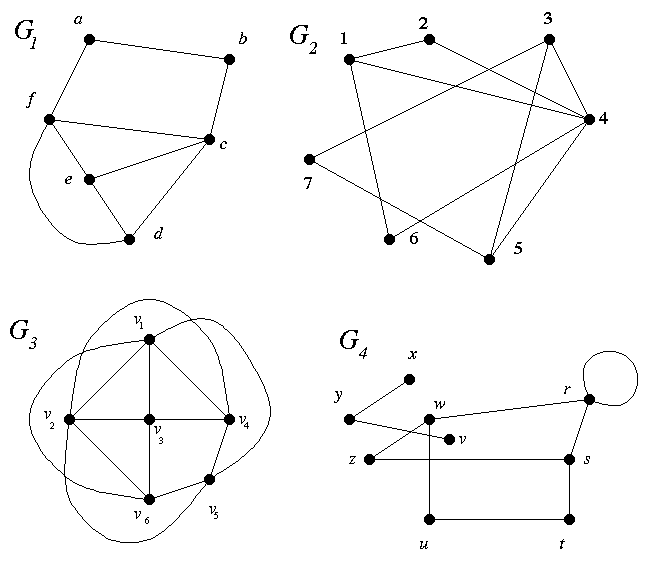
## A1–A5 for G = G1 and G2.
Hand in 2/5:
## A1–A5 for G3, G4. Grading note: I didn't expect proofs in this HW set.
Some terminology about a graph (from the announcements page):
A1. (a) Find a separating set. (b) Find one that is smallest.
A2. (a) Find a disconnecting set. (b) Find one that is smallest.
A3. Write down the degree sequence.
A4. Treat G as a graph in which the vertices stand for people and the edges join pairs who don't get along together, so they can't be on the same committee. What is the largest possible committee?
A5. Is the graph planar, i.e., can you draw it in the plane without crossings?
Due Mon., 2/10:
Read Section 2.1 and the automorphisms handout.
Do for discussion Mon. 2/10:
Hand in Mon., 2/10:
B1. Find a pair of graphs, G and H, that are not isomorphic but which have the same degree sequence and are both connected.
B2. In the graph F of Figure 1.1.16:
B3. Let G be a graph which has a cycle. Let C be a cycle in G. Let a, b be arbitrary vertices in G, and let e be any edge in C. Explain in detail why, if G has a path connecting a to b, so does G − e. Remember that a walk is not necessarily a path.
For Mon. 2/17: Read the chromatic polynomial handout.
Do for discussion Mon. 2/17: ## C1, C4.
Hand in Fri., 2/21:
C1. Let Gn be Kn with one edge deleted. Find the chromatic polynomial of Gn, χGn(k).
C2. Find the chromatic polynomial of a tree of order n. (Recommendation: Start with n = 1, 2, 3. Use induction.)
C3. Find the chromatic polynomial of C4.
C4. How is the chromatic number χ(G) of a graph G related to the chromatic polynomial χG(k)?
C5. Apply the proof method of Theorem 2.1.6 (not the statement of the theorem) to decide whether the following graphs are or are not bipartite.
Homework Set IV (2/7)
Always remember to check the announcements page for corrections to the textbook.
1.3, ## 4, 5, 7.
2.1, # 3.
1.3, ## 6, 12, 13, 20.
2.1, ## 1, 2.
## B1, B2.
Problem Set B
Homework Set V (2/14)
Starting now, I will give 4 bonus points for LaTeX homework.
## C2, C3, C5.
2.1, ## 3, 4 (corr), 6, 7.
Grading note on 2.1.4: I graded one graph. 4/4 for proving chromatic number, 4/4 for a critical subgraph with the same chromatic number.
Grading note on C5: Each part was graded separately.
Problem Set C
Go to homework index.
For Mon. 2/24: Read Section 2.2 and the line graphs handout.
Do for discussion Wed. 2/26:
Hand in Fri., 2/28:
In general (see homework advice), you should start on our homework well ahead of the due date, because some of the problems are easy but some take a lot of thought, which is best done in pieces, even on successive days. That's particularly true in this set.
D1. Suppose G is a connected graph whose average degree is > 2. (Hint: See page 19.) Prove that it is possible for G to have exactly 2 cycles.
D2. Suppose G is a connected graph whose average degree is 3. (Hint: Use a similar idea to D1, but you have to add something.)
D3. Prove or disprove Alleged Theorem 1.3.B: A graph G is a tree if and only if it is connected and its average degree is < 2.
D4. Is the graph of Figure 2.1.5 critical? Prove. (Don't believe everything you read!)
D5. Is the graph of Figure 2.1.6 critical? Prove.
Homework Set VI (2/23)
Note: Theorem 2.2.4 is invalid for n = 1.
2.1, ## 11, 13, 16, 17. Also 9-10 for K4,4 and O.
2.2, # 5.
## D1, D4.
1.3, ## 10, 21.
2.1, ## 5, 8, 15(a), 19, 20 (see announcement).
2.2, ## 3, 6.
## D2, D3, D5.
Problem Set D
(a) Show that G has at least 4 cycles.
(b) Is 4 the best possible number? Or can you prove that G must have 5 or more cycles? 6 or more?
Go to homework index.
For Mon. 3/3: Read Sections 2.3 and 2.4.
Do for discussion M 3/3:
Do for discussion W 3/5:
Hand in Fri. 3/7:
For M 3/17: Read Section 3.1, pp. 49-51.
E1. Prove there is no 1-factor in the graph of Figure 2.2.6 (a) left, (b) right.
E2. Let V(K2n) = {0, 1, 2, ..., 2n−2, x}, as in Section 2.2. We have a standard way to decompose K2n into 1-factors (see Section 2.2). In K8, which "standard" 1-factor contains the following edge? (For your answer you may list all edges that belong to the 1-factor.)
E3. Prove that, if G is a tree, then its edge chromatic number χ'(G) equals its maximum degree Δ(G).
E4. Find a Hamilton cycle or prove there is none.
E5. Find the line graph of each graph.
E6. Is the line graph regular? If so, what is the degree (i.e, the degree of each vertex)?
E7. Let V(K2n+1) = {0, 1, 2, ..., 2n-1, x}. We have a standard way of decomposing K2n+1 into Hamilton cycles (see Section 2.3). In K11, which "standard" Hamilton cycle contains the edge
E8. Is the graph of Figure 2.1.2 critical? Prove.
MIDTERM EXAM 1: Fri., March 21, covering Chapters 1-2, also chromatic polynomial and line graphs.
Read Section 3.1 for Mon., 3/24. See the corrections for Section 3.1.
Recommendation: To better understand the 4-dimensional cube (or "tesseract"), read the short story "—And He Built a Crooked House".
Do for discussion Wed. 3/26:
Hand in Mon. 3/31:
F2. We define a graph to be connected if for any two vertices, there is a path between them (page 17). A fundamental fact is that, if there is a walk between vertices u and v, then there is a path between them (see Connection Theorem). Prove this. (It is possible that the proof of B3 may suggest an idea.)
F3. Decompose into the fewest possible trails:
F4. Decompose into the fewest possible paths: (a, b, c) from #F3. How do these answers compare to those in F3?
F5. Decide whether the graph is Hamiltonian (i.e., has a Hamilton cycle):
F6. Verify that, in the proof of Theorem 2.3.2, the first two 1-factors unite to form a Hamilton cycle. Your proof should be valid for all n ≥ 2.
F7. Regarding tree decompositions of Kp as mentioned at the bottom of page 39:
F8. Use the proof method of Theorem 3.1.7 (Listing's Theorem) to decompose into the smallest possible number of trails:
F9. (a) Find a graph E which has an Eulerian circuit but no Hamilton cycle.
F10. (Bonus problem.) Exercise 2.4.14 asks you to decompose the Petersen graph into 3 subgraphs isomorphic to each other, that is, they are all isomorphic to some graph H. The bonus question is: How many nonisomorphic graphs H are there, for which this is possible? Each must have 5 edges, since Petersen has 15 edges. This is an open-ended question; see how many H's you can come up with.
For Mon. 3/31 read Section 4.1.
Do for discussion Wed. 4/2 & Fri. 4/4:
Hand in Mon. 4/7:
G1. This question concerns the proof of Theorem 4.1.2* (the base case k = 2 of Turan's Theorem). You are given the "starting" graph G of the proof, which has no triangle.
G2. The uniqueness of the maximum graph in Theorems 4.1.2* and 4.1.2 is not proved in the book.
Read for Mon.-Wed. 4/7-9: Sects. 5.1 (omit derangements and the numbers Dn, beginning at bottom of page 90), 5.2 to top of page 95, 6.2. See the announcements page for the incidence matrix of a directed graph (digraph) and the general idea of flows on a graph (including conservative labelings as a special type), and for our improved characterization of strongly conservative graphs.
Do for discussion Wed. 4/9:
Hand in Wed. 4/16:
Voluntary bonus Challenge Problems, due any time before the final exam:
H0. Find the greatest length of a trail in Km,n when m is even and n is odd. (This is the sole case of #4.2.6 we didn't solve in class.)
H1. Suppose G is a connected digraph with p vertices. Prove that the rank of the incidence matrix M(G) equals p − 1. (See the announcements page for hints.)
H2. Suppose G is a strongly conservative digraph. Then there is an edge labelling f using the numbers 1, 2, ..., q, once each, such that f satisfies Kirchhoff's Current Law (KCL) and also for every integer h, the labelling f+h satisfies KCL. Remember that f+h is the labelling that assigns edge e the label f(e)+h.
H3. Suppose G is a strongly conservative digraph. Then for every vertex v, the number of edges with head at v = the number of edges with tail at v. (Hint: Use #H2.)
H4. The proof that K3,3 is nonconservative suggests possible generalizations.
For Wed. 4/16: Read §§7.1 and 8.1 and the handout on the Matrix-Tree Theorem (MT).
LG means the line graphs handout.
Do for discussion Wed. 4/16:
Do for discussion Fri. 4/18:
Do for discussion Tues. 4/22:
Hand in Wed. 4/23:
I1. G is any connected graph. L(L(G)) = L2(G) is the line graph of the line graph, L3(G) is the line graph of L(L(G)), etc.
MIDTERM EXAM 2: Monday, April 28, covering everything subsequent to Midterm 1.
Read for Wed. 4/30: Sects. 8.2-3. (This is a lot to discuss. Study carefully and come in with many questions.)
Do for discussion Wed. 4/30:
Do for discussion Fri. 5/2:
Hand in Mon. 5/5:
J1. (a) Prove that, if p ≥ 11, then Kp has no decomposition into two planar graphs.
J2. Write a complete proof of the 6-Color Theorem.
J3. (a) Prove Theorem G.
J4. Use Theorem G to do (a, b).
Read Section 9.1. The proofs are optional.
The surprising thing about the proof of Theorem 9.1.6 is that it uses Turán's Theorem!
Do for discussion Wed. 5/7:
5/9, 2-4 p.m. in WH 329.
5/13, 5:40-7:40 p.m. in EB J01.
Homework Set VII (3/2)
Regarding p. 45 on components, see the correction.
The last line on p. 38, the one for (Cn), should read
n-1, n-2, n, n-3, n+1, n-4, ..., 2n-2, 2n-1, x.
(This is equivalent to the printed line, but the printed line doesn't follow the pattern it's supposed to.)
2.3, ## 4, 5-7 (for Q3), 18(a).
2.4, # 10.
## E1(a), E2(a,d).
2.2, # 9.
2.3, ## 8, 10, 12, 18(b).
2.4, ## 2, 8.
## E4(a,b), E5(a,b), E6(a,b).
2.2, ## 4, 10.
2.3, ## 1, 2, 5-7 (for D), 17, 18(c).
2.4, # 4, 22, 25.
## E1(b), E2(b,c), E3, E4(c,d), E5(d), E6(c).
Grading note on 2.2.10: I give 4/4 for showing the two graphs and another 4/4 for also explaining why p=q=4 is the only possibility.
Homework Set VIIa (3/2)
2.3, ## 13.
2.4, ## 7, 12 (corr), 13.
3.1, ## 1, 3.
# E8.
Problem Set E
(a) 23.
(b) 2x.
(c) 36.
(d) 15.
(a) Figure 2.3.4.
(b) Figure 2.3.5. (Hint: there isn't!)
(c) Figure 2.1.6.
(d) Figure 2.3.7.
(a) Pn for n ≥ 1.
(b) Cn for n ≥ 3.
(c) K4.
(d) K4 − edge.
(a) Pn for n ≥ 1.
(b) Cn for n ≥ 3.
(c) Kn for n ≥ 4.
(a) 23 ?
(b) 3x ?
(c) 46 ?
(d) 37 ?
Go to homework index.Homework Set VIII (3/23)
The proofs in 3.1 show you how to construct trails, decompositions, etc.
Sect. 3.1, ## 1-3, 4 (for Q3, K4,4 only), 5, 7, 8, 11, 13.
## F3(a), F4(a), F7(a), F8(a).
Sect. 2.4, # 12 (see correction).
Sect. 3.1, ## 6, 12, 14.
## F2, F3(b,c), F4(b,c), F8(d), F9, F10.
Problem Set F
(a) Fig. 1.2.3 (left).
(b) Fig. 2.1.9.
(c) Fig. 2.2.6 (right).
(a) Fig. 2.1.3.
(b) Fig. 2.4.1, the Petersen graph.
(b) Find a graph H which has a Hamilton cycle but no Eulerian circuit.
Homework Set IX (3/28)
For Fri. 4/4, read Section 5.2.
Sect. 4.1, ## 1, 2, 4, 6.
Sect. 4.2, ## 2(a), 4, 6.
# G1(a), G2(a).
Sect. 4.1, ## 3, 5, 7.
Sect. 4.2, ## 2(b), 3, 5(a).
# G1(b), G2(b).
Problem Set G
(i) Construct the new graph H in the proof of Theorem 4.1.2*. What are your x and W?
(ii) Compare the degrees of the vertices in G and H.
(iii) Compare qG = |E(G)| and qH = |E(H)|. Which is larger? Why is that significant for the proof of the theorem?
(iv) Compare H to the largest possible triangle-free graph on the same number of vertices. How are they similar?
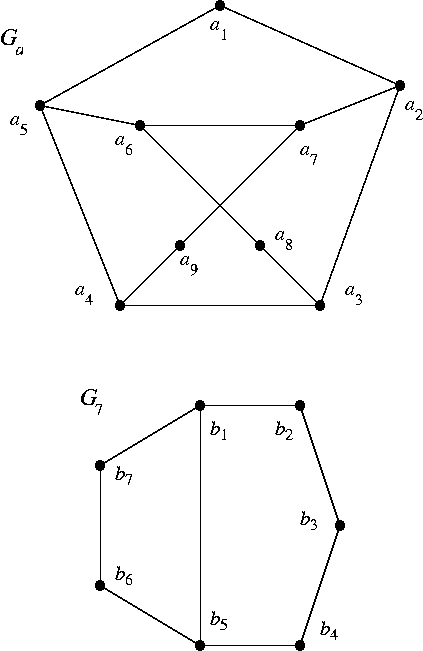
(a) For G = Ga, the Petersen graph with one vertex deleted. (See below.)
(b) For G = G7, shown below.
(a) Prove uniqueness in Theorem 4.1.2*.
(b) Prove uniqueness in Theorem 4.1.2.
Homework Set X (4/6)
§5.1 ## 1, 2,
§6.2 ## 1, 4.
§5.1 ## 3, 12.
§6.2 ## 10, 12, 14.
## H0, H1, H2 (optional), H3 (optional).
# H4, any parts.
Problem Set H
Homework Set XI (4/13)
LG, ## 2, 14.
MT, ## 1, 2.
LG, # 10.
§7.1, ## 1(a), 2(left), 3, 5, 6.
§8.1, ## 1, 2.
§8.1, ## 4, 11, 16.
LG, ## 3, 7(a).
MT, ## 3(a,b)(c), 4.
§7.1, # 2(right).
§8.1, ## 3, 5(left,right), 10, 12.
Optional bonus question: I1.
Problem Set I
Go to homework index.Homework Set XII (4/27)
See Theorem 8.1.A on the relationship between maximal planar graphs and plane triangulations.
Sect. 8.1, # 7.
## J1(a,b).
Sect. 8.2, ## 1, 3.
Sect. 8.3, ## 2, 3.
## J3, J4(a).
Sect. 8.1, # 9.
Sect. 8.2, ## 2, 5, 6.
Sect. 8.3, # 4.
## J1(c), J2, J4(b,c).
Corrections and Additions
Problem Set J
(b) Can K8 be decomposed into two planar graphs?
(c) Prove: if p ≥ 17, then Kp cannot be decomposed into three planar graphs.
(b) What does it say if g = 3?
(c) What does it say if G is bipartite?
(a) Prove: A cubic graph with girth g = 6 cannot be planar.
(b) Prove: A cubic graph with g ≥ 6 cannot be planar.
(c) Can a cubic graph with g = 5 be planar?
Homework Set XIII (4/27)
Recommended (optional) reading: Thickness in §9.2 (pp. 190-193).
Sect. 9.1, ## 1, 5, 6, 7, 11.
Corrections and Additions
d) no edge passes through any vertex;
e) whenever edges intersect, they cross.
Review Session
Final Exam
Go to homework index | announcements | course information | syllabus.