Homework Set III (1/29)

For Mon. 1/31: Read Section 1.3.
Remember to check the announcements page for corrections.

Do for discussion Tues. 2/1:
Sect. 1.1, ## 1, 2, 4(a-c), 6.
Sect. 1.2, # 1, 4, 7.

Do for discussion Wed. 2/2 Fri. 2/4 (Changed due to Wed. cancellation):
Sect. 1.1, # 9.
Sect. 1.2, ## 2, 3, 6, 8.
# C2.

Hand in Fri. 2/4 Mon. 2/7 (Changed due to Wed. cancellation):
Sect. 1.1, ## 3, 4(d), 5, 7, 8.
Sect. 1.2, # 5.
## C1, C3.

Problem Set C

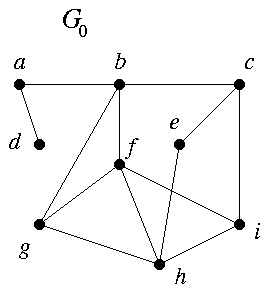
C1. This concerns Theorem 1.1.2 and the example G₀. I follow the book's notation. The sequence
      (S1) (4, 4, 4, 3, 3, 3, 2, 2, 1)
is known to be graphic, because it is the degree sequence of G₀. From (S1) the rule of Theorem 1.1.2 gives
      (S2) (3,3,2,2,3,2,2,1),
which, when rearranged in descending order, is
      (S3) (3,3,3,2,2,2,2,1).

1. In this example what are s, t₁, ..., t_s, n, d₁, ..., d_n? (Give their values.)
2. Label the vertices of G₀ by S, T₁, ..., T_s, D₁, ..., D_n as in the proof of the theorem.) Do this problem for each of the three possible choices of S. [That means parts (b,c,d). – Explanation added Feb. 7.]
3. If you delete vertex S, does the new graph G₀ - S have (S3) as its degree sequence?
4. Use the method in the proof to modify G₀ so that, when you delete S, you do get (S3) as the degree sequence of the new graph.

C2. In the graph F of Figure 1.1.16:

1. Find a longest path P. (Call its endpoints x and y.)
2. Pick an edge e of P which lies in a cycle of F. In F - e, find a path connecting x and y.
3. Pick an edge f of P which does not lie in a cycle of F. In F - f , is there a path connecting x and y?

C3. Let G be a graph which has a cycle. Let C be a cycle in G. Let a, b be arbitrary vertices in G, and let e be any edge in C. Explain in detail why, if G has a path connecting a to b, so does G - e.

      A solution is available here.