Math 381 Homework
Spring 2011

All the assignments are together on this page; each is also on a separate page for easy access and printing.

• Homework Set I and Problem Set A (1/24)   ||   (On a separate page.)
• Homework Set II and Problem Set B (1/24)   ||   (On a separate page.)
• Homework Set III and Problem Set C (1/29)   ||   (On a separate page.)
• Homework Set IV and Problem Set D (2/4)   ||   (On a separate page.)
• Homework Sets V and Va and Problem Sets E and EE (2/12,14)   ||   (On a separate page.)
• Homework Set VI and Problem Set F (2/24)   ||   (On a separate page.)
• Homework Set VII and Problem Set G (3/3-4)   ||   (On a separate page.)
• Homework Sets VIII and VIIIa and Problem Set H (3/10,12,15)   ||   (On a separate page.)
• Homework Set IX and Problem Set I (3/30)   ||   (On a separate page.)
• Homework Set X and Problem Set J (4/5, 8)   ||   (On a separate page.)
• Homework Set XI and Problem Set K (4/15)   ||   (On a separate page.)
• Homework Set XII and Problem Set L (5/3, 9, 11)   ||   (On a separate page.)
• Homework Set XIII and Problem Set M (5/11)   ||   (On a separate page.)

Good Advice and General Instructions
on homework problems

Go to announcements | course information | syllabus | homework index.

Graph Theory Homework: Complete

Homework Set I (1/24)

Due Tues., 1/25:
Do ## A1, A2, A4 for G = G₁ (do this first) and G₂, G₄.
Also, read to the middle of page 9 (changed) in the textbook.
Also, read the course information page and the homework instructions.

Due Wed. 1/26:
      # A3 (again, do G₁ first).

Hand in Wed. 1/26:
      ## A1–A4 for G₃.

Problem Set A

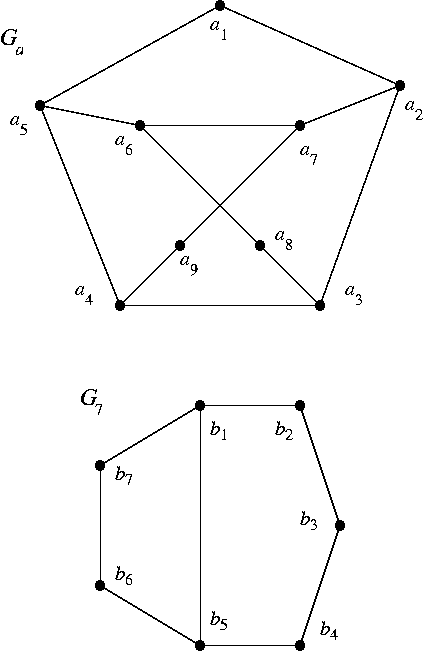
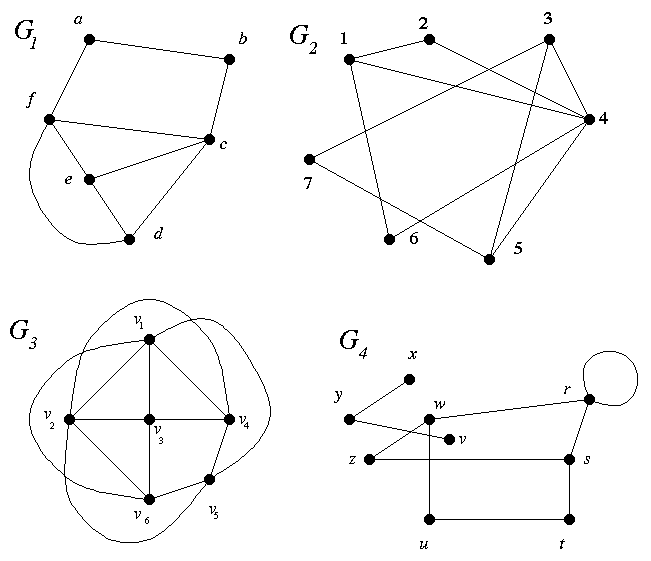
Some terminology about a graph (from the announcements page):

• Order: the number of vertices.
• Size: the number of edges.
• Separating set: a set of vertices whose removal leaves a disconnected graph.
• Disconnecting set: a set of vertices edges whose removal leaves a disconnected graph.

A1. (a) Find a separating set. (b) Find one that is smallest.

A2. (a) Find a disconnecting set. (b) Find one that is smallest.

A3. Write down the degree sequence of G = G₁, G₂, G₃. (Omit G₄.)

A4. Treat G as a graph in which the vertices stand for people and the edges join pairs who don't get along together, so they can't be on the same committee. What is the largest possible committee?

Homework Set II (1/24, 26)

Homework Set III (1/29)

For Mon. 1/31: Read Section 1.3.
Remember to check the announcements page for corrections.

Do for discussion Tues. 2/1:
      Sect. 1.1, ## 1, 2, 4(a-c), 6.
      Sect. 1.2, # 1, 4, 7.

Do for discussion Wed. 2/2 Fri. 2/4 (Changed due to Wed. cancellation):
      Sect. 1.1, # 9.
      Sect. 1.2, ## 2, 3, 6, 8.
      # C2.

Hand in Fri. 2/4:
      Sect. 1.1, ## 3, 4(d), 5, 7, 8.
      Sect. 1.2, # 5.
      ## C1, C3.

Problem Set C

C1. This concerns Theorem 1.1.2 and the example G₀. I follow the book's notation. The sequence
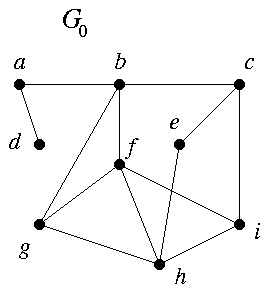
      (S1) (4, 4, 4, 3, 3, 3, 2, 2, 1)
is known to be graphic, because it is the degree sequence of G₀. From (S1) the rule of Theorem 1.1.2 gives
      (S2) (3,3,2,2,3,2,2,1),
which, when rearranged in descending order, is
      (S3) (3,3,3,2,2,2,2,1).

1. In this example what are s, t₁, ..., t_s, n, d₁, ..., d_n? (Give their values.)
2. Label the vertices of G₀ by S, T₁, ..., T_s, D₁, ..., D_n as in the proof of the theorem.) Do this problem for each of the three possible choices of S.
3. If you delete vertex S, does the new graph G₀ - S have (S3) as its degree sequence?
4. Use the method in the proof to modify G₀ so that, when you delete S, you do get (S3) as the degree sequence of the new graph.

C2. In the graph F of Figure 1.1.16:

1. Find a longest path P. (Call its endpoints x and y.)
2. Pick an edge e of P which lies in a cycle of F. In F - e, find a path connecting x and y.
3. Pick an edge f of P which does not lie in a cycle of F. In F - f , is there a path connecting x and y?

C3. Let G be a graph which has a cycle. Let C be a cycle in G. Let a, b be arbitrary vertices in G, and let e be any edge in C. Explain in detail why, if G has a path connecting a to b, so does G - e.

      A solution is available here.

Homework Set IV (2/4)

• The definition of a cycle on p. 16 is valid for n ≥ 3 but not for n = 1 or 2.
• In the proof of Theorem 1.3.5, at the top of p. 20, insert the sentence: "Then follow P₂ back to v₁." before "Then we have a cycle."
• In Exercise 2.1 # 4, you should find
  (a) any critical subgraph;
  (b) a critical subgraph whose chromatic number equals that of the whole graph.
• The graph I in Figure 1.2.5 is the one without a label. (It's the icosahedral graph.)

Problem Set D

D1. Suppose the average degree of a graph G is > 2. [Note: This should have said G is connected. – 2/18]
(a) Prove that G contains at least 2 cycles.
(b) Prove that it is possible for G to have exactly 2 cycles.

      A solution is available here. (Hint for D2: Use a similar idea, but you have to add something.)

D2. Suppose G is a connected graph whose average degree is 3.
(a) Show that G has at least 4 cycles.
(b) Is 4 the best possible number? Or can you prove that G must have 5 or more cycles? 6 or more?

D3. Find the chromatic number χ(G) where G is the graph in Figure 2.1.5.

D4. Is the graph of Figure 2.1.5 critical? Prove. (Don't believe everything you read!)

D5. Is the graph of Figure 2.1.6 critical? Prove.

Homework Set V (2/12)

• Theorem 2.2.4 is valid only for n ≥ 2.

Problem Set E

E1. Prove there is no 1-factor in the graph of Figure 2.2.6 (a) left, (b) right.

E2. Is the graph of Figure 2.1.2 critical? Prove.

TEST I will be on Wednesday, Feb. 23, due to the Presidential Holiday on Monday.

Homework Set Va (2/14)

Homework Set VI (2/24)

F2. Prove that, if G is a tree, then its edge chromatic number χ'(G) equals its maximum degree Δ(G).

F3. Find a Hamilton cycle or prove there is none.
(a) Figure 2.3.4.
(b) Figure 2.3.5. (Hint: there isn't!)
(c) Figure 2.1.6.
(d) Figure 2.3.7.

F4. Let V(K_2n+1) = {0, 1, 2, ..., 2n-1, x}. We have a standard way of decomposing K_2n+1 into Hamilton cycles (see Section 2.3). In K₁₁, which "standard" Hamilton cycle contains the edge
(a) 23 ?
(b) 3x ?
(c) 46 ?
(d) 37 ?

Homework Set VII (3/4)

See the corrections for Section 3.1.

Problem Set G

G1. Decompose into the fewest possible trails:
(a) Fig. 1.2.3 (left).
(b) Fig. 2.1.9.
(c) Fig. 2.2.6 (right).

G2. Decompose into the fewest possible paths: (a, b, c) from #G1.

G3. Decide whether the graph is Hamiltonian (i.e., has a Hamilton cycle):
(a) Fig. 2.1.3.
(b) Fig. 2.4.1, the Petersen graph.

G4. Verify that, in the proof of Theorem 2.3.2, the first two 1-factors unite to form a Hamilton cycle. Your proof should be valid for all n ≥ 2.

Homework Set VIII (3/10,12)

Do for discussion Tues. 3/15:
      Sect. 3.2, ## 1-3, 8.
      ## H1, H2, H5(a), H6(a).
And continued from last week: 2.4 # 12 (see correction), and 3.1 ## 8, 13.

Do for discussion Wed. 3/16:
      Sect. 3.2, ## 4, 6.
      ## H5(b,c), H6(b,c).

Hand in Fri. 3/18:
      Sect. 3.2, ## 5.
      ## H3, H4, H5(d), H6(d).

Homework Set VIIIa (3/12,15)

For Fri. 3/18: Read Section 3.3. (This will not be tested. We'll discuss infinite graphs, just to see the weird differences.)

Additional topic for Fri. 3/18: Line graphs. (This is not in the book. It will not be on Test II but it will probably be on Test III.)

Problem Set H

H1. (a) Find a graph E which has an Eulerian circuit but no Hamilton cycle.
    (b) Find a graph H which has a Hamilton cycle but no Eulerian circuit.

H2. Produce a decomposition of Fig. 3.2.8 into two 2-factors, using the method of proof of Theorem 3.1.4.

H3. Prove that K_p can be decomposed into p - 1 paths P₁, P₂, ..., P_p-1 for all values of p, not only the even values to which Theorem 2.3.4 applies.

H4. For ambitious students, prove rigorously:
    Lemma H4. In a pseudograph G, if there is a trail with endpoints a and b, then there is a path with endpoints a and b.

H5. Use the proof method of Theorem 3.2.4 to decompose into subgraphs isomorphic to P₃ :

1. the Petersen graph, Fig. 1.1.13,
2. the icosahedral graph I in Fig. 1.2.5,
3. Fig. 2.3.4,
4. the Tutte graph, Fig. 2.3.5.

H6. Use the proof method of Theorem 3.1.7 (Listing's Theorem) to decompose into the smallest possible number of trails:

1. the Petersen graph, Fig. 1.1.13,
2. Fig. 2.3.6,
3. Fig. 2.3.7,
4. the Grötzsch graph, Fig. 2.1.6.

H7. (Optional: research problem.) We know some cubic graphs can be decomposed into P₃ subgraphs (e.g., Figs. 2.4.1-2), and some cannot (e.g., Fig. 2.2.6). The counterexample (Fig. 2.2.6) has a bridge, in fact it has three. Must every counterexample have a bridge? That is, can we say that every cubic graph which is connected and has no bridges can be decomposed into P₃ subgraphs?

Homework Set IX and Problem Set I (3/30)

For Fri. 4/1: Read the handouts on graph automorphisms (Aut) and line graphs (LG).

For Mon. 4/4: Read Sects. 4.1 and 4.2.

Do for discussion Tues. 4/5:
      ## LG.2, LG.3, LG.4; ## Aut.1, Aut.2.
      Sect. 4.1, ## 1, 2, 4, 6.
      Sect. 4.2, ## 2(a), 3.
      # I1(a).

Do for discussion Wed. 4/6:
      # LG.9; # Aut.4.
      Sect. 4.1, ## 7, 8.
      Sect. 4.2, ## 2(b), 4, 6.
      # I2(a).

Hand in Fri. 4/8:
      ## LG.7, LG.10; # Aut.5.
      Sect. 4.1, ## 3, 5.
      Sect. 4.2, ## 1, 2(c).
      ## I1(b), I2(b) (I2(b) is postponed to HW X).

Problem Set I

I1. This question concerns the proof of Theorem 4.1.2* (that is, the base case k = 2 of Turan's Theorem). You are given the ``starting'' graph G of the proof, which has no triangle.
(i) Construct the new graph H in the proof of Theorem 4.1.2*. What are your x and W?
(ii) Compare the degrees of the vertices in G and H.
(iii) Compare q_G and q_H. Which is larger? Why is that significant for the proof of the theorem?
(iv) Compare H to the largest possible triangle-free graph on the same number of vertices. How are they similar?

(a) For G = G_a, the Petersen graph with one vertex deleted. (See below.)
(b) For G = G₇, shown below.

I2. The uniqueness of the maximum graph in Theorems 4.1.2* and 4.1.2 is not proved in the book.
(a) Prove uniqueness in Theorem 4.1.2*.
(b) Prove uniqueness in Theorem 4.1.2.

Homework Set X (4/5, 8)

J6. Compare the lower bound p(g) on the order of a g-cage (Theorem 4.2.A) to the actual order of every known g-cage given in the book. Which cages have order equal to p(g)? Which have order greater than p(g)? What does it mean when a g-cage has order > p(g)?

Homework Set XI (4/15)

TEST III will be on Tuesday, May 3.

Problem Set K

K1. Prove that cr(P) ≥ 2, where P is the Petersen graph.

K2. (a) Prove that, if p ≥ 11, then K_p has no decomposition into two planar graphs.
(b) Can K₈ be decomposed into two planar graphs?
(c) Prove: if p ≥ 17, then K_p cannot be decomposed into three planar graphs.

K3. Do both (i) and (ii) for
(a) Fig. 2.3.6.
(b) Fig. 4.2.4.
(c) Fig. 1.3.3.

(i) Is the graph planar?

(ii) Find the crossing number. If you can't calculate it exactly, find out as much as you can about it. For instance, is it = 0 or > 0? Is it = 1? = 2? ≥ 2? ≥ 3? Can you find any upper bound?

K4. Write a complete proof of the 6-Color Theorem: Every planar graph can be colored in 6 colors. (Hint: Try induction on the number of vertices.)

Homework Set XII (5/3, 9)

• Exercise 8.4.9 should read: Find the smallest graph that is planar and regular of degree 3 and has a plane drawing where every edge has the same geometric length.
• See the announcements page for more.

Problem Set L

We define the girth of a forest (such as a tree) to be infinity. Then the girth of a graph is always ≥ 3.

L1.
(a) Prove Theorem G. If G is a planar graph and has girth ≥ g, and if p ≥ 3, then q ≤ [g/(g-2)](p-2).
(b) [ADDED 5/9] What does this say if g = 3?
(c) [ADDED 5/9] What does this say if G is bipartite?

L1'. [ADDED 5/9]
(a) Prove Theorem CR. If G is a graph (not necessarily planar) and has girth ≥ g, and if p ≥ 3, then cr(G) ≥ q - [g/(g-2)](p-2).
(b) What does this say if g = 3?
(c) What does this say if G is bipartite?

L1'' [ADDED 5/11] (This was proved in class, I think. I did prove the case g = 3 in class on 5/6. Feel free to use this theorem if it helps you.)
Theorem SPL. If G is a graph (not necessarily planar) and has girth ≥ g, and if p ≥ 3, then σ(G) ≥ [(g-2]/g] q - (p-2).

L2. Use Theorem G to solve:
(a) Find cr(P), P = Petersen graph.
(b) Find cr(H), H = Heawood graph (Fig. 4.2.4).

L3. Use Theorem G to do (a, b, d).
(a) Prove: A cubic graph with girth g = 6 cannot be planar.
(b) Prove: A cubic graph with g ≥ 6 cannot be planar.
(c) Can a cubic graph with g = 5 be planar?
(d) Find a lower bound on cr(G) when G is cubic and has girth 6.

L4. Prove that cr(K₆ - edge) = 2.

L5. Find θ(P), where P is the Petersen graph.

L6. Prove that θ(K_n) ≥ ceiling[(n+2)/6] for all n ≥ 1.

L7. Let c(G) = the number of cycles in the graph G.
(a) Prove Theorem M: If c(G) < min(c(K₅), c(K_3,3)), then G is planar. (Hint: Use Kuratowski's theorem.)
(b) Evaluate the minimum in Theorem M.
(c) Use (b) to solve Exercise 8.1.3. (If you didn't solve (b), just prove the minimum in (b) is > 3; that should be enough for Exercise 8.1.3.)

L8. Let H = Heawood graph, Fig. 4.2.4.
(a) Prove σ(H) ≥ 2. (Hint: One way is to use Theorem G.)
(b) We know σ(H) ≤ 3. Decide whether σ(H) = 2 or 3.

L9. Prove σ(P) ≥ 2, where P = Petersen graph. (Thus σ(P) = 2, by Exercise 9.3.4.)

Homework Set XIII (5/11)

• "Embedding" a graph is the technical term for drawing it without crossings or any other self-intersection.
• In Sect. 10.3 they often say "circuit of a rotation". What they mean is a region of an embedding of the graph in a surface. "Rotations" are a technical tool that I will avoid. I'll explain this in class.
• See the announcements page for the Euler formulas for graphs embedded in multiple tori.
• Here are pages with diagrams for T₁ (the torus) and T₂ (the double torus), or both T₁ and T₂, that you can use for drawing graphs.

Problem Set M

Problem M1 is basic. The others are for those who enjoy embedding graphs on surfaces (as I do; it's recreational math).

M1. Try to embed non-planar complete graphs in the torus. Start with K₅ (naturally), and if you succeed, try K₆ and then K₇ and then ....

M2. The same as # M1, for the double torus.
Use theorems in Section 10.3 to decide where to stop embedding in the double torus.

M3. Try to embed non-planar complete bipartite graphs in the torus. Start with K_3,3 (naturally), and if you succeed, try K_3,4 and then K_3,5 and K_4,4 – and then (we're getting into summer plans here) ....
Use theorems in Section 10.3 to decide where to stop embedding in the torus.