On this page will be pictures of sculptures I made in Spring 2015. I have five wooden carvings I expect to work on and finish during the spring or summer, and I am making some additional 3D printed designs. Below are pictures of two jewelry size designs recently printed by Shapeways. One is the Mobius Figure Eight Knot (made in matt gold steel) which was shown in several other materials on my Fall 2014 page. The next picture shows that same knot made of Rhodium plated brass (made by Shapeways.com from my design and delivered on August 31, 2015). The other four pictures show a Tubular (3,5) Torus Knot, one made in polished bronze, another made of stainless steel, and the next two are polished bronze steel and polished nickel steel. I made a large silicon bronze version of that (3,5) torus knot as a kinetic sound sculpture in Spring 2010.


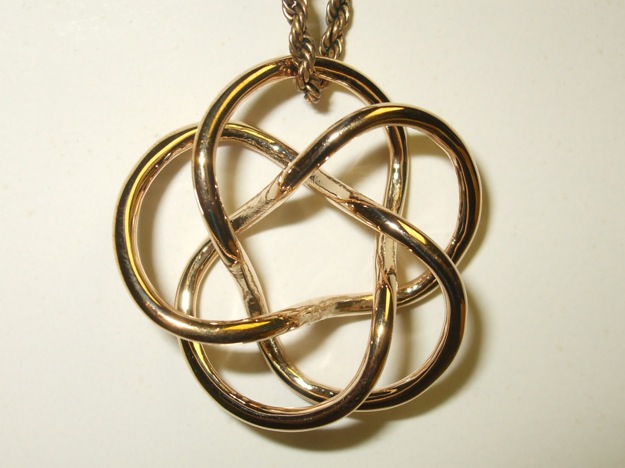



As shown on my Spring and Fall 2014 pages, I made a bronze model of the IHES logo and also a lapel pin version of the logo including the initials. During my visit to IHES in May 2015, I saw that my bronze model (approximately 22" x 24" in size, made from a 1/4" bronze rod) had been mounted on a wall in the lobby area. I took a picture of it (shown below). On April 20, 2016, I received a picture from Philipp Fleig of a bronze dedication plaque which shows that the sculpture was made and donated by me.


I also discussed the lapel pin version with the director and a member of IHES, and was advised to try to reduce the size and simplify the design. I did so, and the following picture shows the result, which is about 2 cm in its largest dimension.

A suggestion was made that I could make a version of my Figure 8 Knot with a torus encircling a cross section, so that the torus would be free to slide along the length of the knot. The following picture shows the result of my efforts to make that happen. At one point the space between the sliding torus and another part of the knot is too close, and the torus is prevented from sliding freely. A slight pressure to flex the knot allows it to continue, but I decided to adjust the design. The new design, shown in the next three pictures, has 5 smaller tori which can slide along the knot, and they all slide freely. This was made by 3D printing at Shapeways.com and was delivered on August 31, 2015.




Last summer I donated one of my bronze cast sculptures, a Mobius Trefoil Knot, to the Albert Einstein Institute (AEI), also called the Max Planck Institute for Gravitational Physics, in Potsdam/Golm, Germany. During my visit, June 1-16, 2015, there was a dedication ceremony, showing how it had been mounted on a specially made wooden pedestal, with a plaque showing the title of the piece, the donor, and a few words. The following pictures show the mounted sculpture, and some of the dedication ceremony, conducted by Prof. Hermann Nicolai, my good friend, collaborator, and a director of AEI.





About a year ago I bought five wooden blocks, all different kinds of wood: Kauri wood, Timborana, Tineo, Cocobolo and Palm Black. The Kauri and Timborana were 3"x6"x6" in size, the Tineo was 2"x6"x6" and the Cocobolo and Palm Black were 2"x4"x4". I prepared them for carving into torus knots by first using a band saw to take off the corners, making cylinders, then I used a hole saw to drill out and save a core cylinder. I made some progress on shaping the core cylinders into the small twisted pieces, and today (July 26, 2015) I finished the polishing of those five twisted cores. There are two pictures showing them below. The smallest is the Palm Black (1.25" tall), next is the thin Cocobolo (2" tall), the middle size is the Tineo (just under 2" tall, 1.5" in diameter), and the two tall ones are the Kauri and the Timborana (both close to 2.5" tall). Kauri wood is very unusual, being thousands of years old, but preserved in bogs (look it up on the internet!). I hope to find time this summer to finish carving at least some of the torus knots from the cylinders with holes. I have recently learned from Don Zagier (MPIM, Bonn, Germany) that the (3,5) torus knot is related to the exceptional Lie algebra of type E8. That Lie algebra has played an important role in my research, so I am happy that I have made several sculptures based on that torus knot.


Below are two pictures torus knots I carved this August. The first is a (3,5) torus knot carved from a 2"x4"x4" block of Black Palm wood, completed on August 9, 2015. The second is a (4,5) torus knot carved from a 2"x4"x4" block of Cocobolo wood, completed on August 30, 2015. As explained above, their centers were used to make two of the twists shown in the last picture. The Black Palm was the smallest twist, and the Cocobolo was the narrow middle size one.


I visited Don Zagier at the Max Planck Institute for Mathematics in Bonn, Germany, June 27-28, and attended two days of the Arbeitstagung. Don told me about many interesting mathematical topics (see above), including some of his recent work involving the unexpected symmetries of a modified (inflated) tetrahedron-like surface given by the equation x2 + y2 + z2 - 2xyz = 1. I decided to try to make it using 3D printing, but wanted to make it hollow, not solid, to reduce the cost and weight. Here are pictures of the results of my efforts, two identical pieces which when glued together at the correct angle, make the desired surface. For each value of z, the cross section is an ellipse, which becomes more excentric as z goes to the upper and lower limits. At those limits, the ellipse degenerates to a line segment, making two of the edges of an ideal tetrahedron which sits inside the surface. The length of that line segment, which is the widest the sculpture gets at the top and and the bottom, is 14mm = 5.5". The cross section when z = 0, the middle of the piece, is a circle whose diameter is 10mm.




To see more types of sculpture I have tried, follow the following links:
Links back to:
Webpage of Alex Feingold,
Department of Mathematical Sciences,
Binghamton University.