On this page will be pictures of sculptures I made in Fall 2016. I made a new design for 3D printing of a Groovy (3,5) Torus Knot, that is, a torus on whose surface has been carved a circular groove in which a steel ball bearing can roll around, following a path which is a (3,5) torus knot. Watching the ball roll around the torus, which is about 3.5" in diameter, you can see it goes around the torus 3 times and through the center hole 5 times before it comes back to a starting point. This is a kinetic visualization of the topology of the knot. It is a companion to my previous design of a Groovy Modius Figure 8 Knot. This version was modified so that a .25" diameter steel ball (separately purchased, not 3D printed) fits and rolls freely in the groove. (See comments on an earlier version at the bottom of the page Sculptures from Spring 2016.)

A second new design for 3D printing completed in Fall 2016 was the Mobius (3,5) Torus Knot with a hypocycloid cross section. I have carved this many times in various kinds of wood, but this design creates the hypocycloid with mathematical precision except at the sharp cusps, which had to be rounded off for 3D printing in small sizes. When printed in metal, 1.25" in diameter, it makes a pendant to be worn as mathematical jewelry. The versions shown in the next four pictures were printed in polished bronze steel, stainless steel, polished nickel steel, and 14k rose gold plated brass. The final picture in this group shows two other copies as well, in strong flexible plastic in two sizes, 1.25" and 3.75".





I modified my design for a lapel pin with the logo of the Institute des Hautes Etudes Scientifique (IHES), so that the entire logo is supported by the backing disk, and so that it does not rotate when it is held by a backing pin. When I get this from Shapeways, I polish the top surface of the logo with fine polishing paper to make the logo shine and stand out from the background disk. The version shown was polished bronze steel and it is about 1" = 2.6 mm in diameter. The second picture shows the back, including the main pin and a secondary small pin to prevent rotation, and the pin clip, made separately. The next picture shows a version printed in raw bronze.



I recently received from Shapeways new copies of my previously designed Mobius Figure 8 Knot Pendant, one is 14K Rose Gold Plated Brass (shown in the first two pictures below), and the other in Polished Bronze Steel.



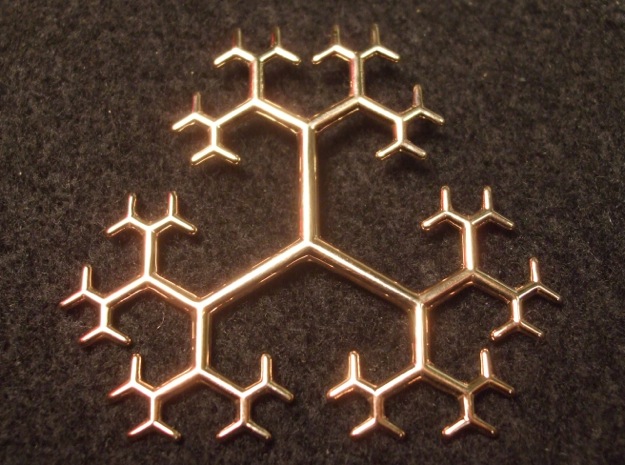
I made a new design based on some research I have been doing in the theory of buildings. This one is a trivalent tree, that is, a graph such that at every vertex three edges are incident. That would make an infinite tree, so this one stops after about four iterations from a central vertex. The ends are sometimes called leaves of the tree. There is a loop on the back so it can be hung from a chain as a pendant. I had three versions printed, one in stainless steel, one in polished bronze steel, and one in 14k rose gold plated brass. They are shown in the following pictures.


I have opened a ``Shapeways Shop", Alex Feingold's Mathematical Art, where some of my designs are now available for purchase as 3D printed objects in various materials (strong flexible plastics in various colors, stainless steel, bronze, silver, etc.). As I perfect more designs, I may make more of them available for sale there. The responsibility for these projects is entirely mine, and I am only using my Binghamton University website to provide information about their commercial availability in the same way that I might provide information about the availability of a textbook or other useful educational resource.
To see more types of sculpture I have tried, follow the following links:
Links back to:
Webpage of Alex Feingold,
Department of Mathematical Sciences,
Binghamton University.