On this page will be pictures of sculptures I made in Spring and Summer 2022. I did not
complete any new sculptures in Fall 2021, so I have not made a webpage for that semester.
I gave a special online course on ``The Mathematical Art of Knots"
to the Binghamton University Lyceum adult learning group
as four 2-hour zoom classes, Jan. 20, 27, Feb. 3, 10, 2022.
On May 30, 2022, I completed another (3,5) torus knot carved from Padauk wood. I started working on it in Fall 2021. It is approximately 5.5" in diameter and 1.5" thick. Below are three pictures of it showing the two sides and an angled front view.



On June 30, 2022, I made two trefoil knots, one from a 1/4" bronze rod 48" long and another from a smaller length of copper wire. The bronze rod knot came out to be about 9" across and a bit flat, very similar to one I made a long time ago. The one made from a heavy copper wire came out to be about 5"x3"x3", more like what I wanted. Since I don't have access to welding equipment any more, I just used solder to join the ends. I made these because a friend expressed a strong interest in trefoil knots and wanted me to make them for him. Below is a picture of these two knots taken from above.

On July 1, 2022, I made another trefoil knot from a 48" length of gauge 4 copper wire. It was much easier to shape than the one made from 1/4" diameter silicon bronze rod. I joined the ends together with solder and a small copper sleeve. The size of the piece came out to be 8"x5"x5". Below are three pictures of it from different angles.
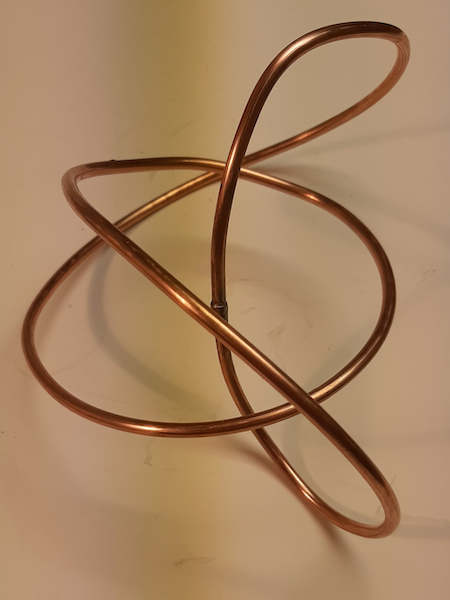


On July 12, 2022, I completed four new wooden torus knot sculptures, two from Purpleheart wood and two from Olivewood. One of the Purpleheart pieces came from a 2"x6"x6" block, and all the others were from 2"x4"x4" blocks. I made two (3,5) torus knots, one from the larger Purpleheart block and one from an Olivewood block. The other two smaller blocks were made into torus links, that is, two (2,1) torus knots linked, which happens when you make a (4,2) torus ``knot". Below are pictures showing these four pieces from various angles and both sides. When they were finished, the actual diameter was smalled than the largest dimension of the original block. The first four pictures show the Olivewood (4,2) torus links.




The next three pictures show the Olivewood (3,5) torus knot.



The next three pictures show the 5.75" diameter Purpleheart (3,5) torus knot.



The next three pictures show the 3.75" diameter Purpleheart (4,2) torus links.



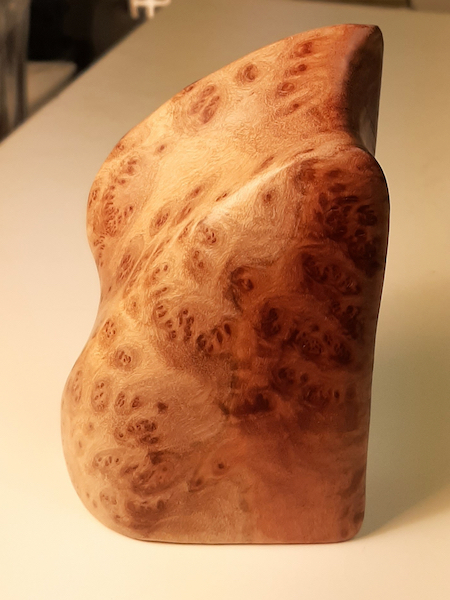
On July 19, 2022, I completed an abstract sculpture carved from a small piece of Australian Red Coolibah Burl, a leftover from a larger piece which was made into a torus knot. The beautiful grain of this burl is the main feature of this piece, which has no particular mathematical significance. I just shaped it to fit into my left hand, which was holding it while I did the carving. The following four pictures show it from different angles in the vertical position which I think is most natural. It is about 4.25"x2.75"x1.5" in size.



On August 5, 2022, I completed the Maple Ambrosia Trefoil Knot carving shown in the following three pictures. The original wood block was 2.5"x8"x8", and the final piece is about 7.5" in diameter and 2" thick. The trefoil knot is formed by the raised edge which goes through the three holes, so this trafoil knot is embedded in a genus 3 surface. The curve, if seen from above follows the pattern usually used to draw a trefoil knot on paper, with alternating over and under crossings. It therefore shows the 3-fold symmetry of the trefoil better than if it had been carved as a (3,2) torus knot.



At various times during 2021-2022, I purchased 3D printed artwork designed by Bathsheba Grossman. She is a brilliant artist and a pioneer in the use of 3D printing to make artwork. The following three pictures show her ``gyroid", ``Seifert surface" (based on the Borromean rings), and her ``120-Cell" (a projection to 3 dimensions of a 4-dimensional object generalizing the pentagon). These were all printed by Shapeways.com in bronze steel.

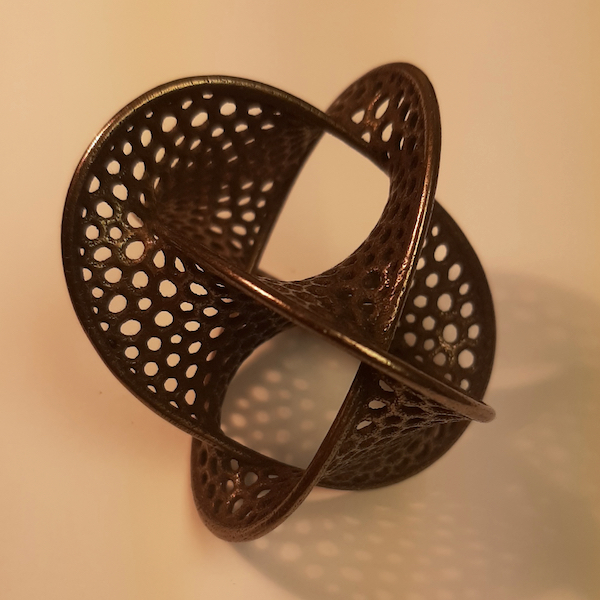

The Lie algebra of type E8 has played an important role in my mathematical research over many years, and has been studied by some of my graduate students as part of their dissertation work. My last Ph.D. student, Joshua Carey, found an artist on Shapeways who created a 3D printd artwork based on the root system of type E8, projected to make a 2-dimensional design. Joshua gave me a copy of that artwork as a gift this summer, 3D printed in gold steel, approximately 3.5" across. Below is a picture of it. Thanks very much, Josh!

In August 23, 2022, I completed carving two more versions of the Trefoil Knot, these made from a piece of Figured Maple which was originally 3.25"x8"x8". I split it into two pieces each of size 1.5"x8"x8", and the final results were about 7.5" in diameter and 1.5" thick. Below are six pictures, three for each carving, showing top, bottom and an angled view. The wood grains on the two pieces are distinctive, even though they both came from the same piece of thicker wood.






To see more types of sculpture I have tried, follow the following links:
Links back to:
Webpage of Alex Feingold,
Department of Mathematical Sciences,
Binghamton University.